
【題目】已知等差數列![]() 的前
的前![]() 項和為
項和為![]() ,等比數列
,等比數列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的通項公式;
的通項公式;
(2)若![]() ,求
,求![]() .
.
【答案】(1)![]() ;(2)21或
;(2)21或![]() .
.
【解析】試題分析:(1)設等差數列![]() 公差為
公差為![]() ,等比數列
,等比數列![]() 公比為
公比為![]() ,由已知條件求出
,由已知條件求出![]() ,再寫出通項公式;(2)由
,再寫出通項公式;(2)由![]() ,求出
,求出![]() 的值,再求出
的值,再求出![]() 的值,求出
的值,求出![]() 。
。
試題解析:設等差數列![]() 公差為
公差為![]() ,等比數列
,等比數列![]() 公比為
公比為![]() 有
有![]() ,即
,即![]() .
.
(1)∵![]() ,結合
,結合![]() 得
得![]() ,
,
∴![]() .
.
(2)∵![]() ,解得
,解得![]() 或3,
或3,
當![]() 時,
時,![]() ,此時
,此時![]() ;
;
當![]() 時,
時,![]() ,此時
,此時![]() .
.
【題型】解答題
【結束】
20
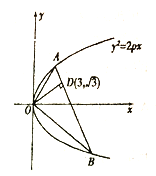
【題目】如圖,已知直線與拋物線![]() 相交于
相交于![]() 兩點,且
兩點,且![]() ,
, ![]() 交
交![]() 于
于![]() ,且點
,且點![]() 的坐標為
的坐標為![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 為拋物線的焦點,
為拋物線的焦點, ![]() 為拋物線上任一點,求
為拋物線上任一點,求![]() 的最小值.
的最小值.
 能考試期末沖刺卷系列答案
能考試期末沖刺卷系列答案科目:高中數學 來源: 題型:
【題目】設函數f′(x)是奇函數f(x)(x∈R)的導函數,f(﹣1)=0,當x>0時,xf′(x)﹣f(x)<0,則使得f(x)>0成立的x的取值范圍是( )
A.(﹣∞,﹣1)∪(0,1)
B.(﹣1,0)∪(1,+∞)
C.(﹣∞,﹣1)∪(﹣1,0)
D.(0,1)∪(1,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列 ![]() 中,公差
中,公差 ![]() ,
, ![]() ,且
,且 ![]() 成等比數列.
成等比數列.
(1)求數列 ![]() 的通項公式;
的通項公式;
(2)若 ![]() 為數列
為數列 ![]() 的前
的前 ![]() 項和,且存在
項和,且存在 ![]() ,使得
,使得 ![]() 成立,求實數
成立,求實數 ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小張經營某一消費品專賣店,已知該消費品的進價為每件40元,該店每月銷售量(百件)與銷售單價x(元/件)之間的關系用下圖的一折線表示,職工每人每月工資為1000元,該店還應交付的其它費用為每月10000元.

(1)把y表示為x的函數;
(2)當銷售價為每件50元時,該店正好收支平衡(即利潤為零),求該店的職工人數;
(3)若該店只有20名職工,問銷售單價定為多少元時,該專賣店可獲得最大月利潤?(注:利潤=收入-支出)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓 ![]() 的左、右焦點分別為
的左、右焦點分別為 ![]() ,上、下頂點分別是
,上、下頂點分別是 ![]() ,點
,點 ![]() 是
是 ![]() 的中點,若
的中點,若 ![]() ,且
,且 ![]() .
.
(1)求橢圓 ![]() 的標準方程;
的標準方程;
(2)過 ![]() 的直線
的直線 ![]() 與橢圓
與橢圓 ![]() 交于不同的兩點
交于不同的兩點 ![]() ,求
,求 ![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x+ ![]() +lnx,a∈R. (Ⅰ)若f(x)在x=1處取得極值,求a的值;
+lnx,a∈R. (Ⅰ)若f(x)在x=1處取得極值,求a的值;
(Ⅱ)若f(x)在區間(1,2)上單調遞增,求a的取值范圍;
(Ⅲ)討論函數g(x)=f'(x)﹣x的零點個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,平面ABEF⊥平面ABC,四邊形ABEF為矩形,AC=BC.O為AB的中點,OF⊥EC. (Ⅰ)求證:OE⊥FC:
(Ⅱ)若 ![]() =
= ![]() 時,求二面角F﹣CE﹣B的余弦值.
時,求二面角F﹣CE﹣B的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com