
【題目】平潭國際“花式風(fēng)箏沖浪”集訓(xùn)隊,在平潭龍鳳頭海濱浴場進行集訓(xùn),海濱區(qū)域的某個觀測點觀測到該處水深![]() (米)是隨著一天的時間
(米)是隨著一天的時間![]() 呈周期性變化,某天各時刻
呈周期性變化,某天各時刻![]() 的水深數(shù)據(jù)的近似值如下表:
的水深數(shù)據(jù)的近似值如下表:
| 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| 1.5 | 2.4 | 1.5 | 0.6 | 1.4 | 2.4 | 1.6 | 0.6 | 1.5 |
(Ⅰ)根據(jù)表中近似數(shù)據(jù)畫出散點圖(坐標(biāo)系在答題卷中).觀察散點圖,從
①![]() , ②
, ②![]() ,③
,③![]()
![]() 中選擇一個合適的函數(shù)模型,并求出該擬合模型的函數(shù)解析式;(Ⅱ)為保證隊員安全,規(guī)定在一天中的5~18時且水深不低于1.05米的時候進行訓(xùn)練,根據(jù)(Ⅰ) 中的選擇的函數(shù)解析式,試問:這一天可以安排什么時間段組織訓(xùn)練,才能確保集訓(xùn)隊員的安全。
中選擇一個合適的函數(shù)模型,并求出該擬合模型的函數(shù)解析式;(Ⅱ)為保證隊員安全,規(guī)定在一天中的5~18時且水深不低于1.05米的時候進行訓(xùn)練,根據(jù)(Ⅰ) 中的選擇的函數(shù)解析式,試問:這一天可以安排什么時間段組織訓(xùn)練,才能確保集訓(xùn)隊員的安全。
【答案】(1) 選②![]() 做為函數(shù)模型,
做為函數(shù)模型, ![]() ;(2) 這一天可以安排早上5點至7點以及11點至18點的時間段組織訓(xùn)練.
;(2) 這一天可以安排早上5點至7點以及11點至18點的時間段組織訓(xùn)練.
才能確保集訓(xùn)隊員的安全.
【解析】試題分析 :(1)先畫出散點圖,可知選②做為函數(shù)模型,同時可求出各參數(shù), ![]() ,
, ![]() 代最值點可求。(2)由(Ⅰ)知:
代最值點可求。(2)由(Ⅰ)知: ![]() ,
,![]() 令
令![]() ,可解得
,可解得![]() 。
。
試題解析:(Ⅰ)根據(jù)表中近似數(shù)據(jù)畫出散點圖,如圖所示:
-
依題意,選②![]() 做為函數(shù)模型,
做為函數(shù)模型,
![]()
![]()
![]()
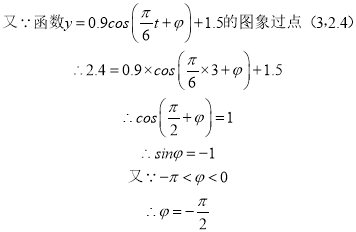
![]()
(Ⅱ)由(Ⅰ)知: ![]()
令![]() ,即
,即![]()
![]()
![]()
![]()
又![]()
![]()
∴這一天可以安排早上5點至7點以及11點至18點的時間段組織訓(xùn)練,
才能確保集訓(xùn)隊員的安全。


科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,我海監(jiān)船在![]() 島海域例行維權(quán)巡航,某時刻航行至
島海域例行維權(quán)巡航,某時刻航行至![]() 處,此時測得其東北方向與它相距
處,此時測得其東北方向與它相距![]() 海里的
海里的![]() 處有一外國船只,且
處有一外國船只,且![]() 島位于海監(jiān)船正東
島位于海監(jiān)船正東![]() 海里處。
海里處。
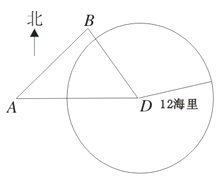
(Ⅰ)求此時該外國船只與![]() 島的距離;
島的距離;
(Ⅱ)觀測中發(fā)現(xiàn),此外國船只正以每小時![]() 海里的速度沿正南方向航行。為了將該船攔截在離
海里的速度沿正南方向航行。為了將該船攔截在離![]() 島
島![]() 海里處,不讓其進入
海里處,不讓其進入![]() 島
島![]() 海里內(nèi)的海域,試確定海監(jiān)船的航向,并求其速度的最小值.
海里內(nèi)的海域,試確定海監(jiān)船的航向,并求其速度的最小值.
(參考數(shù)據(jù): ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
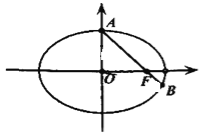
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,上頂點為
,上頂點為![]() ,短軸長為2,
,短軸長為2,![]() 為原點,直線
為原點,直線![]() 與橢圓
與橢圓![]() 的另一個交點為
的另一個交點為![]() ,且
,且![]() 的面積是
的面積是![]() 的面積的3倍.
的面積的3倍.
(1)求橢圓![]() 的方程;
的方程;
(2)直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,若在橢圓
兩點,若在橢圓![]() 上存在點
上存在點![]() ,使
,使![]() 為平行四邊形,求
為平行四邊形,求![]() 取值范圍.
取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直角梯形ABCD中,AD∥BC,∠ADC=90°,A(-3,-10),
B (-2,-1),C(3,4),
(1)求邊AD和CD所在的直線方程;
(2)數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,點
,點![]() 在直線CD上,求證
在直線CD上,求證![]() 為等比數(shù)列.
為等比數(shù)列.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,已知曲線
中,已知曲線![]() (
(![]() 為參數(shù)),在以
為參數(shù)),在以![]() 為極點,
為極點, ![]() 軸正半軸為極軸的極坐標(biāo)系中,曲線
軸正半軸為極軸的極坐標(biāo)系中,曲線![]() ,曲線
,曲線![]() .
.
(1)求曲線![]() 與
與![]() 的交點
的交點![]() 的直角坐標(biāo);
的直角坐標(biāo);
(2)設(shè)點![]() ,
, ![]() 分別為曲線
分別為曲線![]() 上的動點,求
上的動點,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓E: ![]() 的離心率為
的離心率為![]() ,過左焦點作x軸的垂線交橢圓于A、B兩點,且|AB|=1.
,過左焦點作x軸的垂線交橢圓于A、B兩點,且|AB|=1.
(1)求橢圓E的方程;
(2)設(shè)P、Q是橢圓E上兩點,P在第一象限,Q在第二象限,且OP⊥OQ,其中O是坐標(biāo)原點.
當(dāng)P、Q運動時,是否存在定圓O,使得直線PQ都與定圓O相切?若存在,請求出圓O的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,曲線
,曲線![]() 在點
在點![]() 處的切線與直線
處的切線與直線![]() 垂直(其中
垂直(其中![]() 為自然對數(shù)的底數(shù)).
為自然對數(shù)的底數(shù)).
(1)求![]() 的解析式及單調(diào)遞減區(qū)間;
的解析式及單調(diào)遞減區(qū)間;
(2)是否存在常數(shù)![]() ,使得對于定義域內(nèi)的任意
,使得對于定義域內(nèi)的任意![]() ,
, ![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】等比數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,已知對任意的
,已知對任意的![]() ,點
,點![]() 均在函數(shù)
均在函數(shù)![]() (
(![]() 且
且![]() ,
, ![]() 均為常數(shù))的圖象上.
均為常數(shù))的圖象上.
(1)求![]() 的值;
的值;
(2)當(dāng)![]() 時,記
時,記![]() ,證明:對任意的
,證明:對任意的![]() ,不等式
,不等式![]() 成立.
成立.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知四棱柱![]() 的底面是邊長為2的菱形,且
的底面是邊長為2的菱形,且![]() ,
,![]() ⊥平面
⊥平面![]() ,
,![]() ,設(shè)
,設(shè)![]() 為
為![]() 的中點.
的中點.

(1)求證:![]() ⊥平面
⊥平面![]() ;
;
(2)點![]() 在線段
在線段![]() 上,且
上,且![]() 平面
平面![]() ,求平面
,求平面![]() 和平面
和平面![]() 所成銳角的余弦值.
所成銳角的余弦值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com