
��߅������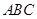 ��߅�L(zh��ng)��3���c(di��n)
��߅�L(zh��ng)��3���c(di��n)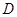 ��
��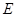 �քe��߅
�քe��߅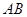 ��
��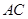 �ϵ��c(di��n)���ҝM��
�ϵ��c(di��n)���ҝM��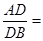
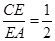 ����D1��������
����D1��������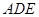 ��
��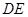 ����
����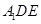 ��λ�ã�ʹ�����
��λ�ã�ʹ�����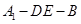 ��ֱ����ǣ��B�Y(ji��)
��ֱ����ǣ��B�Y(ji��)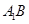 ��
��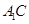 ����D2����
����D2����
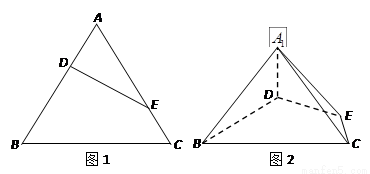
��1�����C��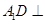 ƽ��
ƽ��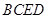 ��
��
��2���ھ���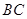 ���Ƿ�����c(di��n)
���Ƿ�����c(di��n) ��ʹֱ��
��ʹֱ��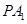 �cƽ��
�cƽ��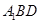 ���ɵĽǞ�
���ɵĽǞ�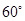 �������ڣ����
�������ڣ����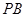 ���L(zh��ng)���������ڣ�Ո(q��ng)�f�����ɣ�
���L(zh��ng)���������ڣ�Ո(q��ng)�f�����ɣ�
��1��ԔҊ��������2�����ڣ���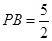 .
.
��������
ԇ�}��������1���@��һ��(g��)�C���}�������������Ҷ�����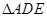 ���
���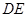 ���L(zh��ng)�ȣ��Y(ji��)�Ϲ��ɶ����C��
���L(zh��ng)�ȣ��Y(ji��)�Ϲ��ɶ����C��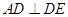 ���Ķ����ۯB��(du��)��(y��ng)����
���Ķ����ۯB��(du��)��(y��ng)����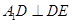 ��Ȼ������ƽ��
��Ȼ������ƽ��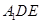
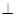 ƽ��
ƽ��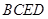 ���Y(ji��)��ƽ���cƽ�洹ֱ�����|(zh��)�����C��
���Y(ji��)��ƽ���cƽ�洹ֱ�����|(zh��)�����C��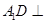 ƽ��
ƽ��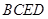 ����2������1�����ã�1���е���ʾ�l���f��
����2������1�����ã�1���е���ʾ�l���f��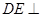 ƽ��
ƽ�� ��
��
Ȼ�����^�c(di��n)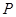 ��
��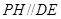 ������Եõ�
������Եõ�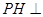 ƽ��
ƽ�� ���Ķ�
���Ķ�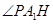 ��ֱ��
��ֱ��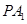 �cƽ��
�cƽ�� ���ɵĽǣ��M(j��n)�����@
���ɵĽǣ��M(j��n)�����@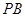 ���L(zh��ng)���M(j��n)��Ӌ(j��)�㣻����2�����ÿ��g���������ȼ��O(sh��)�c(di��n)
���L(zh��ng)���M(j��n)��Ӌ(j��)�㣻����2�����ÿ��g���������ȼ��O(sh��)�c(di��n)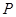 ������(bi��o)�����ã�1���е���ʾ�l���f��
������(bi��o)�����ã�1���е���ʾ�l���f��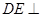 ƽ��
ƽ�� ����
����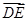 ҕ��ƽ��
ҕ��ƽ�� ��һ��(g��)��������Ȼ������
��һ��(g��)��������Ȼ������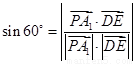 �_���c(di��n)
�_���c(di��n)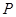 ������(bi��o)���M(j��n)��Ӌ(j��)��
������(bi��o)���M(j��n)��Ӌ(j��)��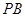 ���L(zh��ng)��.
���L(zh��ng)��.
ԇ�}�������C������1����?y��n)��߅�?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2013092000190384191803/SYS201309200020062666930057_DA.files/image020.png">��߅�L(zh��ng)��3����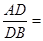
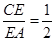 ��
��
����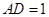 ��
��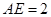 ��
��
�ڡ�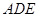 �У�
��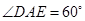 ��
��
�����Ҷ�����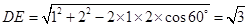 ��
��
��?y��n)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2013092000190384191803/SYS201309200020062666930057_DA.files/image028.png">������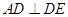 ��
��
�ۯB����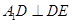 ��
2��
��
2��
��?y��n)����?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2013092000190384191803/SYS201309200020062666930057_DA.files/image029.png">��ֱ����ǣ�����ƽ��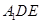
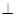 ƽ��
ƽ��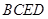 ��
3��
��
3��
��ƽ��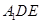
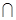 ƽ��
ƽ��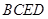
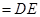 ��
��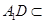 ƽ��
ƽ��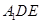 ��
��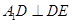 ��
��
����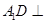 ƽ��
ƽ��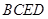 ��
4��
��
4��
��2���ⷨ1�����O(sh��)�ھ���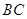 �ϴ����c(di��n)
�ϴ����c(di��n)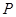 ��ʹֱ��
��ʹֱ��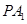 �cƽ��
�cƽ�� ���ɵĽǞ�
���ɵĽǞ� ��
��
��D����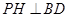 ���c(di��n)
���c(di��n) ���B�Y(ji��)
���B�Y(ji��)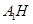 ��
��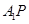 �� 5��
�� 5��

�ɣ�1����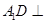 ƽ��
ƽ��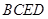 ����
����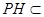 ƽ��
ƽ��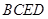 ��
��
����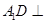
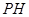 ��
6��
��
6��
��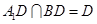 ��
��
����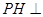 ƽ��
ƽ�� ��
7��
��
7��
����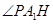 ��ֱ��
��ֱ��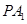 �cƽ��
�cƽ�� ���ɵĽǣ�
8��
���ɵĽǣ�
8��
�O(sh��)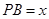
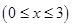 ���t
���t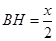 ��
��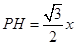 ��
9��
��
9��
��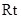 ��
��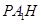 ��
��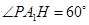 ������
������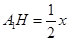 ��
10��
��
10��
��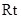 ��
��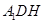 ��
��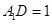 ��
��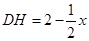 ��
11��
��
11��
��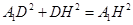 ��
��
��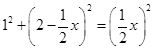 ��
12��
��
12��
���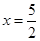 ���M��
���M��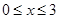 �������}�⣮
13��
�������}�⣮
13��
�����ھ���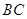 �ϴ����c(di��n)
�ϴ����c(di��n)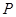 ��ʹֱ��
��ʹֱ��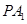 �cƽ��
�cƽ�� ���ɵĽǞ�
���ɵĽǞ� ���˕r(sh��)
���˕r(sh��)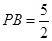 �� 14��
�� 14��
�ⷨ2���ɣ�1�����C������֪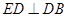 ��
��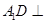 ƽ��
ƽ��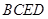 ��
��
��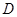 ������(bi��o)ԭ�c(di��n)�����侀
������(bi��o)ԭ�c(di��n)�����侀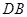 ��
��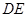 ��
�� �քe��
�քe��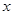 �S��
�S��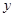 �S��
�S��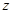 �S�������S���������gֱ������(bi��o)ϵ
�S�������S���������gֱ������(bi��o)ϵ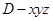 ��D��
5��
��D��
5��

�O(sh��)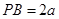
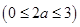 ��
��
�t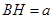 ��
��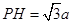 ��
��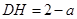 �� 6��
�� 6��
����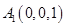 ��
��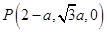 ��
��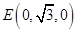 �� 7��
�� 7��
����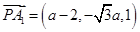 ��
8��
��
8��
��?y��n)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2013092000190384191803/SYS201309200020062666930057_DA.files/image076.png">ƽ�� ��
��
����ƽ�� ��һ��(g��)��������
��һ��(g��)��������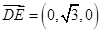 ��
9��
��
9��
��?y��n)�ֱ��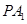 �cƽ��
�cƽ�� ���ɵĽǞ�
���ɵĽǞ� ��
��
����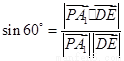 10��
10��
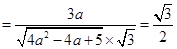 ��
11��
��
11��
���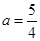 ��
12��
��
12��
��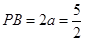 ���M��
���M��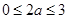 �������}�⣮
13��
�������}�⣮
13��
�����ھ���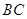 �ϴ����c(di��n)
�ϴ����c(di��n)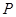 ��ʹֱ��
��ʹֱ��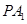 �cƽ��
�cƽ�� ���ɵĽǞ�
���ɵĽǞ� ���˕r(sh��)
���˕r(sh��)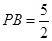 �� 14��
�� 14��
���c(di��n)��ֱ���cƽ�洹ֱ�����Ҷ�����ֱ���cƽ�����ɵĽǡ����g����



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ������ʡ�������У2012�ø���12��(li��n)����(sh��)�W(xu��)����ԇ�} �}�ͣ�044
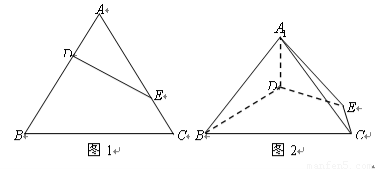
��֪AB��ƽ��ACD��DE��ƽ��ACD����ACD���߅�����Σ�߅�L(zh��ng)��2a��AD��DE��2AB��F(xi��n)��CD�����c(di��n)��
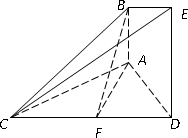
(1)���C��AF��ƽ��BCE��
(2)���C��ƽ��BCE��ƽ��CDE��
(3)��ֱ��BF��ƽ��BCE���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ��2013-2014�W(xu��)�갲��ʡ��У�����о���(hu��)����2��(li��n)�����Ɣ�(sh��)�W(xu��)ԇ���������棩 �}�ͣ�����}
��߅������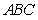 ��߅�L(zh��ng)��3,�c(di��n)
��߅�L(zh��ng)��3,�c(di��n)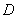 ��
��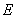 �քe��߅
�քe��߅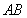 ��
��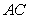 �ϵ��c(di��n),�ҝM��
�ϵ��c(di��n),�ҝM��
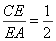 (��D1).����
(��D1).����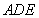 ��
��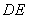 ������
������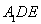 ��λ��,ʹ�����
��λ��,ʹ�����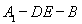 ��ֱ�����,�B�Y(ji��)
��ֱ�����,�B�Y(ji��)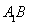 ��
��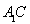 (��D2).
(��D2).
���������C: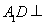 ƽ��
ƽ�� ;
;
�������ھ��� ���Ƿ�����c(di��n)
���Ƿ�����c(di��n)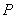 ,ʹֱ��
,ʹֱ��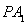 �cƽ��
�cƽ��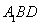 ���ɵĽǞ�
���ɵĽǞ�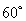 ?������,���
?������,���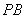 ���L(zh��ng),��������,Ո(q��ng)�f������.
���L(zh��ng),��������,Ո(q��ng)�f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ��2011-2012�W(xu��)�����ʡ����и���12����У(li��n)�����Ɣ�(sh��)�W(xu��)ԇ�� �}�ͣ�����}
����С�}�M��12�֣���֪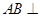 ƽ��
ƽ��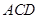 ��
��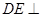 ƽ��
ƽ��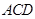 ����
����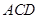 ���߅�����Σ�߅�L(zh��ng)��2a��
���߅�����Σ�߅�L(zh��ng)��2a��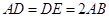 ��
��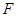 ��
��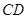 �����c(di��n).
�����c(di��n).
��1�����C��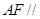 ƽ��
ƽ��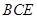 ��
��
��2�����C��ƽ��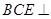 ƽ��
ƽ��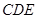 ��
��
��3����ֱ��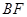 ��ƽ��
��ƽ��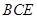 ���ɽǵ�����ֵ.
���ɽǵ�����ֵ.

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
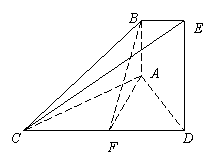
��֪![]() ƽ��
ƽ��![]() ��
��![]() ƽ��
ƽ��![]() ����
����![]() ���߅�����Σ�߅�L(zh��ng)��2a��
���߅�����Σ�߅�L(zh��ng)��2a��![]() ��
��![]() ��
��![]() �����c(di��n).
�����c(di��n).
��1�����C��![]() ƽ��
ƽ��![]() ��
��
��2�����C��ƽ��![]() ƽ��
ƽ��![]() ��
��
��3����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵ.
���ɽǵ�����ֵ.
 |
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com