Question

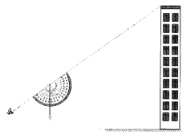
【題目】數學興趣小組為了測量校園外一座“不可到達”建筑物的高度，采用“兩次測角法”，并自制了測量工具：將一個量角器放在復印機上放大4倍復印，在中心處綁上一個鉛錘，用于測量樓頂仰角（如圖）；推動自行車來測距（輪子滾動一周為1.753米）.該小組在操場上選定A點，此時測量視線和鉛錘線之間的夾角在量角器上度數為37°；推動自行車直線后退，輪子滾動了10卷達到B點，此時測量視線和鉛錘線之間的夾角在量角器上度數為53°.測量者站立時的“眼高”為1.55m，根據以上數據可計算得該建筑物的高度約為___________米.（精確到0.1）

參考數據：，

Answer 1

【答案】31.6

【解析】

由題意畫出簡圖，設，即可得、，利用即可得解.

由題意畫出簡圖，如圖：

由題意可得，，，

所以，

，

設，則在中，，

在中，，

所以，解得，

所以該建筑的高度約為米.

故答案為：31.6.