
【題目】已知數列![]() 是等差數列,數列
是等差數列,數列![]() 是等比數列,且
是等比數列,且![]() ,
,![]() 的前n項和為
的前n項和為![]() .若
.若![]() 對任意的
對任意的![]() 恒成立.
恒成立.
(1)求數列![]() ,
,![]() 的通項公式;
的通項公式;
(2)若數列![]() 滿足
滿足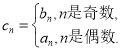 問:是否存在正整數
問:是否存在正整數![]() ,使得
,使得![]() ,若存在求出
,若存在求出![]() 的值,若不存在,說明理由;
的值,若不存在,說明理由;
(3)若存在各項均為正整數公差為![]() 的無窮等差數列
的無窮等差數列![]() ,滿足
,滿足![]() ,且存在正整數
,且存在正整數![]() ,使得
,使得![]() 成等比數列,求
成等比數列,求![]() 的所有可能的值.
的所有可能的值.
【答案】(1)![]() ,
,![]() .(2)存在,
.(2)存在,![]() 的值為5和
的值為5和![]() .(3)
.(3)![]() 或
或![]() .
.
【解析】
(1)由題意可知![]() ,從而有
,從而有![]() ,做差得到
,做差得到![]() ,代入基本量計算可求出數列
,代入基本量計算可求出數列![]() ,
,![]() 的通項公式. (2)討論
的通項公式. (2)討論![]() 為奇數和偶數兩種情況,分別代入求解計算. (3)設
為奇數和偶數兩種情況,分別代入求解計算. (3)設![]() 的公差為
的公差為![]() ,則
,則![]() 且
且![]() ,若
,若![]() ,則
,則![]() 肯定成立,只需討論
肯定成立,只需討論![]() 時的情況即可.
時的情況即可.
(1)當![]() 時,
時,![]() ,由
,由![]() ,得
,得![]() ;
;
由![]() 得
得![]() ①,當
①,當![]() 時有:
時有:![]() ②,
②,
由②-①得![]() .
.
分別令![]() 可得:
可得:![]() ,
,![]() .設
.設![]() 的公差為
的公差為![]() ,
,![]() 的公比為
的公比為![]() ,
,
則 解得
解得![]() 或
或
經檢驗![]() 符合條件,
符合條件, 不合題意,舍去.
不合題意,舍去.
故![]() ,
,![]() .
.
(2)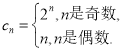
當![]() 是奇數時,由
是奇數時,由![]() ,可得
,可得![]() ,即
,即![]() ,
,
所以![]() ,解得
,解得![]() ,
,
考慮到![]() 在正整數集上分別單調遞增和遞減,
在正整數集上分別單調遞增和遞減,
故不存在其他解,即![]() 是惟一解.
是惟一解.
當![]() 是偶數時,由
是偶數時,由![]() 可得:
可得:![]() ,
,
即![]() ,
,![]() 是偶數符合條件.
是偶數符合條件.
綜上![]() 的值為5和
的值為5和![]() .
.
(3)由(1)![]() ,設
,設![]() 的公差為
的公差為![]() ,則
,則![]() 且
且![]() ,
,
當![]() 時,顯然成立;
時,顯然成立;
當![]() 時,
時,![]()
所以![]() ,
,![]() ,
,
由![]() ,得
,得![]() ,
,
即![]() ,
,
所以![]() ,
,
因為![]() ,所以
,所以![]() ,
,
即![]() ,
,
所以![]()
故![]()
![]() ,
,
由![]() ,得
,得![]() ,
,
從而要使![]() ,只要
,只要![]() ,
,
又![]() ,
,
綜上,![]() .
.


 習題精選系列答案
習題精選系列答案科目:高中數學 來源: 題型:
【題目】如圖所示,折線圖和條形圖分別為某位職員2018年與2019年的家庭總收入各種用途所占比例的統計圖,已知2018年的家庭總收入為10萬元,2019年的儲蓄總量比2018年的儲蓄總量減少了10%,則下列說法:
①2019年家庭總收入比2018年增長了8%;
②年衣食住的總費用與2018年衣食住的總費相同;
③2019年的旅行總費用比2018年增加了2800元;
④2019年的就醫總費用比2018年增長了5%
其中正確的個數為( )
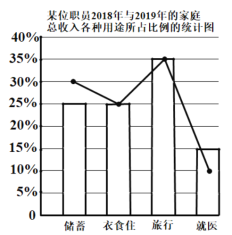
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數,
為參數,![]() 為直線
為直線![]() 的傾斜角),以坐標原點
的傾斜角),以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系,曲線
軸正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出曲線![]() 的直角坐標方程,并求
的直角坐標方程,并求![]() 時直線
時直線![]() 的普通方程;
的普通方程;
(2)直線![]() 和曲線
和曲線![]() 交于
交于![]() 、
、![]() 兩點,點
兩點,點![]() 的直角坐標為
的直角坐標為![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (其中
(其中![]() 是常數,且
是常數,且![]() ),曲線
),曲線![]() 在
在![]() 處的切線方程為
處的切線方程為![]() .
.
(1)求![]() 的值;
的值;
(2)若存在![]() (其中
(其中![]() 是自然對數的底),使得
是自然對數的底),使得![]() 成立,求
成立,求![]() 的取值范圍;
的取值范圍;
(3)設![]() ,若對任意
,若對任意![]() ,均存在
,均存在![]() ,使得方程
,使得方程![]() 有三個不同的實數解,求實數
有三個不同的實數解,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
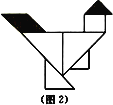
【題目】七巧板是一種古老的中國傳統智力玩具,是由七塊板組成.而這七塊板可拼成許多圖形,人物、動物、建筑物等,在18世紀,七巧板流傳到了國外,至今英國劍橋大學的圖書館里還珍藏著一部《七巧圖譜》.若用七巧板(圖1為正方形),拼成一只雄雞(圖2),在雄雞平面圖形上隨機取一點,則恰好取自雄雞雞頭或雞尾(陰影部分)的概率為( )
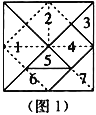
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩位同學參加詩詞大賽,各答3道題,每人答對每道題的概率均為![]() ,且各人是否答對每道題互不影響.
,且各人是否答對每道題互不影響.
(Ⅰ)用![]() 表示甲同學答對題目的個數,求隨機變量
表示甲同學答對題目的個數,求隨機變量![]() 的分布列和數學期望;
的分布列和數學期望;
(Ⅱ)設![]() 為事件“甲比乙答對題目數恰好多2”,求事件
為事件“甲比乙答對題目數恰好多2”,求事件![]() 發生的概率.
發生的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com