
設函數 (其中
(其中 >0,
>0, ),且f(x)的圖象在y軸右側的第一個最高點的橫坐標為
),且f(x)的圖象在y軸右側的第一個最高點的橫坐標為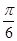 .
.
(1)求 的值;
的值;
(2)如果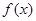 在區間
在區間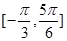 的最小值為
的最小值為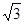 ,求
,求 的值.
的值.
(1)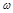 =
= ;(2)a=
;(2)a=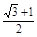 .
.
解析試題分析:(1)對函數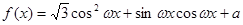 進行化簡,得到f(x)==sin(2
進行化簡,得到f(x)==sin(2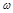 x+
x+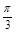 )+
)+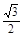 +a,得到2
+a,得到2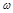 ·
·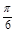 +
+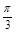 =
= ,即可求出
,即可求出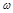 的值;(2)由(1)知f(x)=sin(2
的值;(2)由(1)知f(x)=sin(2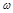 x+
x+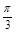 )+
)+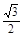 +a,當x∈
+a,當x∈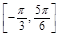 時,x+
時,x+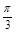 ∈
∈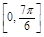 ,故-
,故- ≤sin(x+
≤sin(x+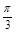 )≤1,從而f(x)在
)≤1,從而f(x)在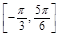 上取得最小值-
上取得最小值- +
+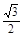 +a,因此,由題設知-
+a,因此,由題設知- +
+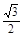 +a=
+a=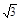 ,即可求出a的值.
,即可求出a的值.
解:(1) f(x)=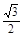 cos2
cos2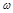 x+
x+ sin2
sin2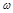 x+
x+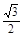 +a .2
+a .2
=sin(2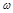 x+
x+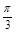 )+
)+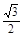 +a ..4
+a ..4
依題意得2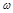 ·
·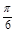 +
+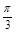 =
= 解得
解得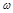 =
= .6
.6
(2) 由(1)知f(x)=sin(2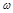 x+
x+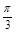 )+
)+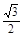 +a
+a
又當x∈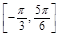 時,x+
時,x+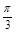 ∈
∈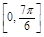 8
8
故- ≤sin(x+
≤sin(x+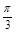 )≤1 ..10
)≤1 ..10
從而f(x)在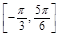 上取得最小值-
上取得最小值- +
+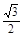 +a
+a
因此,由題設知- +
+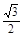 +a=
+a=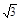 故a=
故a=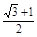 .12
.12
考點:1.三角函數恒等變換;2.三角函數的最值.


 名校提分一卷通系列答案
名校提分一卷通系列答案 課程達標測試卷闖關100分系列答案
課程達標測試卷闖關100分系列答案 新卷王期末沖刺100分系列答案
新卷王期末沖刺100分系列答案 全能闖關100分系列答案
全能闖關100分系列答案科目:高中數學 來源: 題型:解答題
已知向量m=(sin x,1),n= ,函數f(x)=(m+n)·m.
,函數f(x)=(m+n)·m.
(1)求函數f(x)的最小正周期T及單調遞增區間;
(2)已知a,b,c分別為△ABC內角A,B,C的對邊,A為銳角,a=2 ,c=4,且f(A)是函數f(x)在
,c=4,且f(A)是函數f(x)在 上的最大值,求△ABC的面積S.
上的最大值,求△ABC的面積S.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com