
【題目】設(shè)拋物線y2=2x的焦點(diǎn)為F,過點(diǎn)M( ![]() ,0)的直線與拋物線相交于A,B兩點(diǎn),與拋物線的準(zhǔn)線相交于C,|BF|=2,則△BCF和△ACF的面積之比為 .
,0)的直線與拋物線相交于A,B兩點(diǎn),與拋物線的準(zhǔn)線相交于C,|BF|=2,則△BCF和△ACF的面積之比為 .
【答案】![]()
【解析】解:∵拋物線方程為y2=2x,∴焦點(diǎn)F的坐標(biāo)為( ![]() ,0), 準(zhǔn)線方程為x=﹣
,0), 準(zhǔn)線方程為x=﹣ ![]() ,
,
如圖,設(shè)A(x1 , y1),B(x2 , y2),
過A,B分別向拋物線的準(zhǔn)線作垂線,垂足分別為E,N,
則|BF|=x2+ ![]() =2,
=2,
∴x2= ![]() ,
,
把x2= ![]() 代入拋物線y2=2x,得,y2=﹣
代入拋物線y2=2x,得,y2=﹣ ![]() ,
,
∴直線AB過點(diǎn)M( ![]() ,0)與(
,0)與( ![]() ,﹣
,﹣ ![]() )
)
方程為 ![]() x+(
x+( ![]() ﹣
﹣ ![]() )y﹣3=0,代入拋物線方程,解得,x1=2
)y﹣3=0,代入拋物線方程,解得,x1=2
∴|AE|=2+ ![]() =
= ![]() ,
,
∵在△AEC中,BN∥AE,
∴|BC|:|AC|=|BN|:|AE|=2: ![]() =
= ![]() ,
,
△BCF和△ACF的面積之比為: ![]() |BC|h:
|BC|h: ![]() |AC|h=
|AC|h= ![]()
所以答案是: ![]()


 明天教育課時(shí)特訓(xùn)系列答案
明天教育課時(shí)特訓(xùn)系列答案 浙江新課程三維目標(biāo)測評課時(shí)特訓(xùn)系列答案
浙江新課程三維目標(biāo)測評課時(shí)特訓(xùn)系列答案 周周清檢測系列答案
周周清檢測系列答案 輕巧奪冠周測月考直通高考系列答案
輕巧奪冠周測月考直通高考系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本小題滿分14分)如圖,四棱錐![]() 的底面ABCD 是平行四邊形,平面PBD⊥平面 ABCD, PB=PD,
的底面ABCD 是平行四邊形,平面PBD⊥平面 ABCD, PB=PD, ![]() ⊥
⊥![]() ,
, ![]() ⊥
⊥![]() ,
, ![]() ,
, ![]() 分別是
分別是![]() ,
, ![]() 的中點(diǎn),連結(jié)
的中點(diǎn),連結(jié)![]() .求證:
.求證:

(1)![]() ∥平面
∥平面![]() ;
;
(2)![]() ⊥平面
⊥平面![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,一個(gè)水輪的半徑為4m,水輪圓心O距離水面2m,已知水輪每分鐘轉(zhuǎn)動(dòng)5圈,如果當(dāng)水輪上點(diǎn)P從水中浮現(xiàn)時(shí)(圖中點(diǎn)p0)開始計(jì)算時(shí)間. 
(1)將點(diǎn)p距離水面的高度z(m)表示為時(shí)間t(s)的函數(shù);
(2)點(diǎn)p第一次到達(dá)最高點(diǎn)大約需要多少時(shí)間?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,當(dāng)∠xOy=α,且α∈(0, ![]() )∪(
)∪( ![]() ,π)時(shí),定義平面坐標(biāo)系xOy為α﹣仿射坐標(biāo)系.在α﹣仿射坐標(biāo)系中,任意一點(diǎn)P的斜坐標(biāo)這樣定義:
,π)時(shí),定義平面坐標(biāo)系xOy為α﹣仿射坐標(biāo)系.在α﹣仿射坐標(biāo)系中,任意一點(diǎn)P的斜坐標(biāo)這樣定義: ![]() 、
、 ![]() 分別為與x軸、y軸正向相同的單位向量,若
分別為與x軸、y軸正向相同的單位向量,若 ![]() =x
=x ![]() +y
+y ![]() ,則記為
,則記為 ![]() =(x,y).現(xiàn)給出以下說法:
=(x,y).現(xiàn)給出以下說法:
①在α﹣仿射坐標(biāo)系中,已知 ![]() =(1,2),
=(1,2), ![]() =(3,t),若
=(3,t),若 ![]() ∥
∥ ![]() ,則t=6;
,則t=6;
②在α﹣仿射坐標(biāo)系中,若 ![]() =(
=( ![]() ,
, ![]() ),若
),若 ![]() =(
=( ![]() ,﹣
,﹣ ![]() ),則
),則 ![]()
![]() =0;
=0;
③在60°﹣仿射坐標(biāo)系中,若P(2,﹣1),則| ![]() |=
|= ![]() ;
;
其中說法正確的有 . (填出所有說法正確的序號)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列{![]() }中,
}中,![]() ,且
,且![]() 對任意正整數(shù)都成立,數(shù)列{
對任意正整數(shù)都成立,數(shù)列{![]() }的前n項(xiàng)和為Sn。
}的前n項(xiàng)和為Sn。
(1)若![]() ,且
,且![]() ,求a;
,求a;
(2)是否存在實(shí)數(shù)k,使數(shù)列{![]() }是公比不為1的等比數(shù)列,且任意相鄰三項(xiàng)
}是公比不為1的等比數(shù)列,且任意相鄰三項(xiàng)![]() 按某順序排列后成等差數(shù)列,若存在,求出所有k值,若不存在,請說明理由;
按某順序排列后成等差數(shù)列,若存在,求出所有k值,若不存在,請說明理由;
(3)若![]() 。
。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在三棱錐P-ABC中,D為AB的中點(diǎn)。

(1)與BC平行的平面PDE交AC于點(diǎn)E,判斷點(diǎn)E在AC上的位置并說明理由如下:
(2)若PA=PB,且△PCD為銳角三角形,又平面PCD⊥平面ABC,求證:AB⊥PC。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
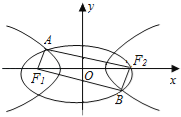
【題目】如圖F1、F2是橢圓C1:![]() +y2=1與雙曲線C2的公共焦點(diǎn),A、B分別是C1、C2在第二、四象限的公共點(diǎn),若四邊形AF1BF2為矩形,則C2的離心率是( )
+y2=1與雙曲線C2的公共焦點(diǎn),A、B分別是C1、C2在第二、四象限的公共點(diǎn),若四邊形AF1BF2為矩形,則C2的離心率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】用數(shù)學(xué)歸納法證明12+22+…+(n﹣1)2+n2+(n﹣1)2+…+22+12═ ![]() 時(shí),由n=k的假設(shè)到證明n=k+1時(shí),等式左邊應(yīng)添加的式子是( )
時(shí),由n=k的假設(shè)到證明n=k+1時(shí),等式左邊應(yīng)添加的式子是( )
A.(k+1)2+2k2
B.(k+1)2+k2
C.(k+1)2
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某地區(qū)2009年至2015年農(nóng)村居民家庭人均純收入y(單位:千元)的數(shù)據(jù)如表:
年份 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
年份代號t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均純收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y關(guān)于t的線性回歸方程;
(2)利用(1)中的回歸方程,分析2009年至2015年該地區(qū)農(nóng)村居民家庭人均純收入的變化情況,并預(yù)測該地區(qū)2017年農(nóng)村居民家庭人均純收入.
附:回歸直線的斜率和截距的最小二乘估計(jì)公式分別為: 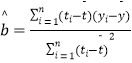 .
. ![]() .
.
參考數(shù)據(jù):(﹣3)×(﹣1.4)+(﹣2)×(﹣1)+(﹣1)×(﹣0.7)+1×0.5+2×0.9+3×1.6=14.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com