
【題目】已知函數f(x)= ![]() (a>0,且a≠1)在R上單調遞減,且關于x的方程|f(x)|=2﹣x恰好有兩個不相等的實數解,則a的取值范圍是( )
(a>0,且a≠1)在R上單調遞減,且關于x的方程|f(x)|=2﹣x恰好有兩個不相等的實數解,則a的取值范圍是( )
A.(0, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]∪{
]∪{ ![]() }
}
D.[ ![]() ,
, ![]() )∪{
)∪{ ![]() }
}
【答案】C
【解析】解:y=loga(x+1)+1在[0,+∞)遞減,則0<a<1,函數f(x)在R上單調遞減,則: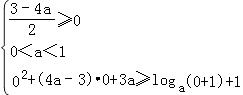 ;
;
解得, ![]() ;
;
由圖象可知,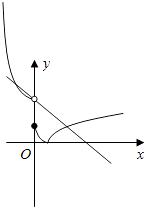
在[0,+∞)上,|f(x)|=2﹣x有且僅有一個解,
故在(﹣∞,0)上,|f(x)|=2﹣x同樣有且僅有一個解,
當3a>2即a> ![]() 時,聯立|x2+(4a﹣3)x+3a|=2﹣x,
時,聯立|x2+(4a﹣3)x+3a|=2﹣x,
則△=(4a﹣2)2﹣4(3a﹣2)=0,
解得a= ![]() 或1(舍去),
或1(舍去),
當1≤3a≤2時,由圖象可知,符合條件,
綜上:a的取值范圍為[ ![]() ,
, ![]() ]∪{
]∪{ ![]() },
},
故選:C.
利用函數是減函數,根據對數的圖象和性質判斷出a的大致范圍,再根據f(x)為減函數,得到不等式組,利用函數的圖象,方程的解的個數,推出a的范圍.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0, ![]() ),其部分圖象如圖所示. (I)求f(x)的解析式;
),其部分圖象如圖所示. (I)求f(x)的解析式;
(II)求函數 ![]() 在區間
在區間 ![]() 上的最大值及相應的x值.
上的最大值及相應的x值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足:對任意的n∈N*均有an+1=kan+3k﹣3,其中k為不等于0與1的常數,若ai∈{﹣678,﹣78,﹣3,22,222,2222},i=2,3,4,5,則滿足條件的a1所有可能值的和為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正四棱柱ABCD﹣A1B1C1D1 , AB=a,AA1=2a,E,F分別是棱AD,CD的中點.
(1)求異面直線BC1與EF所成角的大小;
(2)求四面體CA1EF的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C以原點為中心,左焦點F的坐標是(﹣1,0),長軸長是短軸長的 ![]() 倍,直線l與橢圓C交于點A與B,且A、B都在x軸上方,滿足∠OFA+∠OFB=180°;
倍,直線l與橢圓C交于點A與B,且A、B都在x軸上方,滿足∠OFA+∠OFB=180°; 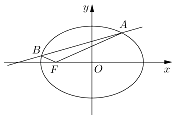
(1)求橢圓C的標準方程;
(2)對于動直線l,是否存在一個定點,無論∠OFA如何變化,直線l總經過此定點?若存在,求出該定點的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數f(x)=ax2﹣4x+c的值域為[0,+∞).
(1)判斷此函數的奇偶性,并說明理由;
(2)判斷此函數在[ ![]() ,+∞)的單調性,并用單調性的定義證明你的結論;
,+∞)的單調性,并用單調性的定義證明你的結論;
(3)求出f(x)在[1,+∞)上的最小值g(a),并求g(a)的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示:有三根針和套在一根針上的若干金屬片.按下列規則,把金屬片從一根針上全部移到另一根針上.
(1)每次只能移動一個金屬片;
(2)在每次移動過程中,每根針上較大的金屬片不能放在較小的金屬片上面.將n個金屬片從1號針移到3號針最少需要移動的次數記為f(n);
①f(3)=;
②f(n)= . 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足:a1+2a2+…+nan=4﹣ ![]() .
.
(1)求數列{an}的通項公式;
(2)若bn=(3n﹣2)an , 求數列{bn}的前n項和Sn .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com