【題目】現安排6名同學前往4所學校進行演講，要求甲、乙兩同學不能前往同一個學校，每個學校都有人前往，每人只前往一個學校，則滿足上述要求的不同安排方案數為________．（用數字作答）
激活思維智能訓練課時導學練系列答案科目：高中數學 來源： 題型：
【題目】已知點
是橢圓
的左、右焦點，點
是該橢圓上一點，若當
時，
面積達到最大，最大值為
.
（1）求橢圓
的標準方程；
（2）設
為坐標原點，是否存在過左焦點
的直線
，與橢圓交于
兩點，使得
的面積為
？若存在，求出直線的方程；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某少兒游泳隊需對隊員進行限時的仰臥起坐達標測試.已知隊員的測試分數
與仰臥起坐
個數
之間的關系如下：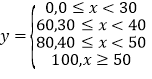
；測試規則：每位隊員最多進行三組測試，每組限時1分鐘，當一組測完，測試成績達到60分或以上時，就以此組測試成績作為該隊員的成績，無需再進行后續的測試，最多進行三組；根據以往的訓練統計，隊員“喵兒”在一分鐘內限時測試的頻率分布直方圖如下：
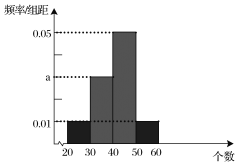
（1）計算
值；
（2）以此樣本的頻率作為概率，求
①在本次達標測試中，“喵兒”得分等于
的概率；
②“喵兒”在本次達標測試中可能得分的分布列及數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給出下面類比推理：
①“若2a<2b，則a<b”類比推出“若a2<b2，則a<b”；
②“(a＋b)c＝ac＋bc(c≠0)”類比推出“
(c≠0)”；
③“a，b∈R，若a－b＝0，則a＝b”類比推出“a，b∈C，若a－b＝0，則a＝b”；
④“a，b∈R，若a－b>0，則a>b”類比推出“a，b∈C，若a－b>0，則a>b(C為復數集)”．
其中結論正確的個數為( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，設拋物線
的焦點為F，點P是半橢圓
上的一點，過點P作拋物線C的兩條切線，切點分別為A、B，且直線PA、PB分別交y軸于點M、N．
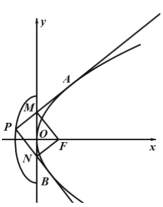
（1）證明：
；
（2）求
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線C的頂點在坐標原點，焦點在坐標軸上.
（1）若拋物線C經過點
，求C的標準方程；
（2）拋物線C的焦點
（m是大于零的常數），若過點F的直線與C交于
兩點，
，求
面積的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
