【題目】已知函數
（Ⅰ）求函數的定義域，并證明在定義域上是奇函數；
（Ⅱ）若
恒成立，求實數
的取值范圍；
（Ⅲ）當
時，試比較
與
的大小關系．
【答案】（Ⅰ）函數的定義域為
，
在定義域上是奇函數。
（Ⅱ）
（Ⅲ）
時,
成立.
【解析】
試題（1）判斷函數奇偶性的方法：1、先求出函數定義域若關于原點對稱,則進行第二步；若不關于原點對稱則為非奇非偶函數2、再判斷
與
的關系，如果相等則是偶函數，如若互為相反數則是奇函數，若不能確定則為非奇非偶函數（2）對于恒成立的問題，常用到以下兩個結論：（1）
，（2）
（3）證明不等式可以利用作差法，也可構造函數，利用函數的單調性解決
試題解析：（Ⅰ）由
，解得
或
，
∴ 函數的定義域為
當
時，
∴
在定義域上是奇函數。
（Ⅱ）由
時，
恒成立，
∴
∴
在成立
令
，，由二次函數的性質可知
時函數單調遞增，
時函數單調遞減，
時，
∴
（Ⅲ）
=
構造函數
，
當
時，
，∴
在
單調遞減，
當
（
）時，
.
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】曲線
與兩坐標軸的交點都在圓
上，圓與
軸正半軸、
軸正半軸分別交于
，
兩點.
（Ⅰ）求圓的方程；
（Ⅱ）過點
作直線
與圓交于
，
兩點，是否存在使得
與
共線，如果存在求直線的方程，若不存在請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的左、右焦點分別為
，上頂點為
，
的面積為1，且橢圓
的離心率為
.
（1）求橢圓的標準方程；
（2）點
在橢圓上且位于第二象限，過點
作直線
，過點
作直線
，若直線
的交點
恰好也在橢圓上，求點的坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在直三棱柱ABC-A1B1C1中，D，E分別為AB，BC的中點，點F在側棱B1B上，且
， 
.
求證：（1）直線DE
平面A1C1F；
（2）平面B1DE⊥平面A1C1F.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本題滿分13分）
某食品廠進行蘑菇的深加工，每公斤蘑菇的成本20元，并且每公斤蘑菇的加工費為
元（為常數，且
，設該食品廠每公斤蘑菇的出廠價為
元（
），根據市場調查，銷售量
與
成反比，當每公斤蘑菇的出廠價為30元時，日銷售量為100公斤.
（Ⅰ）求該工廠的每日利潤
元與每公斤蘑菇的出廠價元的函數關系式；
（Ⅱ）若
，當每公斤蘑菇的出廠價為多少元時，該工廠的利潤最大，并求最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列
是等比數列，有下列四個命題：①
是等比數列；②
是等比數列；③
是等比數列；④
是等比數列，其中正確命題的序號是( )
A.②④B.③④C.②③④D.①②③④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2018年10月28日，重慶公交車墜江事件震驚全國，也引發了廣大群眾的思考——如何做一個文明的乘客.全國各地大部分社區組織居民學習了文明乘車規范.
社區委員會針對居民的學習結果進行了相關的問卷調查，并將得到的分數整理成如圖所示的統計圖.
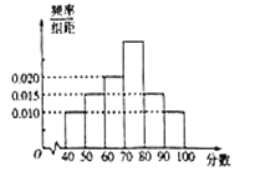
（Ⅰ）求得分在
上的頻率；
（Ⅱ）求社區居民問卷調查的平均得分的估計值；（同一組中的數據以這組數據所在區間中點的值作代表）
（Ⅲ）以頻率估計概率，若在全部參與學習的居民中隨機抽取5人參加問卷調查，記得分在
間的人數為
，求的分布列.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，函數
.
（1）求函數
在
上的最小值；
（2）函數
，若
在其定義域內有兩個不同的極值點，求a的取值范圍；
（3）記的兩個極值點分別為
，且
.已知
，若不等式
恒成立，求
的取值范圍.注：
為自然對數的底數.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對某產品1至6月份銷售量及其價格進行調查，其售價x和銷售量y之間的一組數據如下表所示：
月份i | 1 | 2 | 3 | 4 | 5 | 6 |
單價 | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
銷售量 | 11 | 10 | 8 | 6 | 5 | 14 |
（1）根據1至5月份的數據，求出y關于x的回歸直線方程；
（2）若由回歸直線方程得到的估計數據與剩下的檢驗數據的誤差不超過0.5元，則認為所得到的回歸直線方程是理想的，試問所得回歸直線方程是否理想？
（3）預計在今后的銷售中，銷售量與單價仍然服從（1）中的關系，且該產品的成本是2.5元/件，為獲得最大利潤，該產品的單價應定為多少元？（利潤=銷售收入-成本）.
參考公式：回歸方程
，其中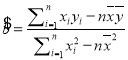
.
參考數據：
，
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
