
【題目】已知圓![]() 與直線
與直線![]() 相切.
相切.
(1)求圓![]() 的方程;
的方程;
(2)過點![]() 的直線
的直線![]() 截圓
截圓![]() 所得弦長為
所得弦長為![]() ,求直線
,求直線![]() 的方程;
的方程;
(3)設(shè)圓![]() 與
與![]() 軸的負半抽的交點為
軸的負半抽的交點為![]() ,過點
,過點![]() 作兩條斜率分別為
作兩條斜率分別為![]() 的直線交圓
的直線交圓![]() 于
于![]() 兩點,且
兩點,且![]() ,證明:直線
,證明:直線![]() 過定點,并求出該定點坐標.
過定點,并求出該定點坐標.
科目:高中數(shù)學 來源: 題型:
【題目】《中華人民共和國道路交通安全法》規(guī)定:車輛駕駛員血液酒精濃度在20~80mg/100ml(不含80)之間,屬于酒后駕車;在80mg/100ml(含80)以上時,屬于醉酒駕車.某市公安局交通管理部門在某路段的一次攔查行動中,依法檢查了300輛機動車,查處酒后駕車和醉酒駕車的駕駛員共20人,檢測結(jié)果如表:
酒精含量(mg/100ml) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70)[] | [70,80) | [80,90) | [90,100] |
人數(shù) | 3 | 4 | 1 | 4 | 2 | 3 | 2 | 1 |
(Ⅰ)繪制出檢測數(shù)據(jù)的頻率分布直方圖(在圖中用實線畫出矩形框即可);
(Ⅱ)求檢測數(shù)據(jù)中醉酒駕駛的頻率,并估計檢測數(shù)據(jù)中酒精含量的眾數(shù)、平均數(shù).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖①所示,四邊形![]() 為等腰梯形,
為等腰梯形,![]() ,且
,且![]() 于點
于點![]() 為
為![]() 的中點.將
的中點.將![]() 沿著
沿著![]() 折起至
折起至![]() 的位置,得到如圖②所示的四棱錐
的位置,得到如圖②所示的四棱錐![]() .
.
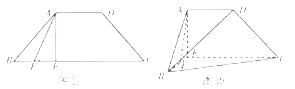
(1)求證:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】我國是世界上嚴重缺水的國家,某市政府為了鼓勵居民節(jié)約用水,計劃調(diào)整居民生活用水收費方案,擬確定一個合理的月用水量標準![]() (噸)、一位居民的月用水量不超過
(噸)、一位居民的月用水量不超過![]() 的部分按平價收費,超過
的部分按平價收費,超過![]() 的部分按議價收費,為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數(shù)據(jù)按照
的部分按議價收費,為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數(shù)據(jù)按照![]() 分成9組,制成了如圖所示的頻率分布直方圖.
分成9組,制成了如圖所示的頻率分布直方圖.

(1)求直方圖中![]() 的值;
的值;
(2)設(shè)該市有30萬居民,估計全市居民中月均用量不低于3噸的人數(shù),并說明理由;
(3)若該市政府希望使85%的居民每月的用水量不超過標準![]() (噸),估計
(噸),估計![]() 的值,并說明理由.
的值,并說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知點![]() 是直線
是直線![]() 與橢圓
與橢圓![]() 的一個公共點,
的一個公共點,![]() 分別為該橢圓的左右焦點,設(shè)
分別為該橢圓的左右焦點,設(shè)![]() 取得最小值時橢圓為
取得最小值時橢圓為![]() .
.
(I)求橢圓![]() 的方程;
的方程;
(II)已知![]() 是橢圓
是橢圓![]() 上關(guān)于
上關(guān)于![]() 軸對稱的兩點,
軸對稱的兩點,![]() 是橢圓
是橢圓![]() 上異于
上異于![]() 的任意一點,直線
的任意一點,直線![]() 分別與
分別與![]() 軸交于點
軸交于點![]() ,試判斷
,試判斷![]() 是否為定值,并說明理由.
是否為定值,并說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列各式:
(1)![]() ;
;
(2)已知![]() ,則
,則![]() ;
;
(3)函數(shù)![]() 的圖象與函數(shù)
的圖象與函數(shù)![]() 的圖象關(guān)于y軸對稱;
的圖象關(guān)于y軸對稱;
(4)函數(shù)![]() 的定義域是R,則m的取值范圍是
的定義域是R,則m的取值范圍是![]() ;
;
(5)函數(shù)![]() 的遞增區(qū)間為
的遞增區(qū)間為![]() .
.
正確的有______________________.(把你認為正確的序號全部寫上)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)集合A={x|-1≤x≤2},B={x|m-1≤x≤2m+1},已知BA.
(1)當x∈N時,求集合A的子集的個數(shù);
(2)求實數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)函數(shù)![]() .
.
(1)若![]() 是函數(shù)
是函數(shù)![]() 的極值點,1和
的極值點,1和![]() 是函數(shù)
是函數(shù)![]() 的兩個不同零點,且
的兩個不同零點,且![]() ,求
,求![]() .
.
(2)若對任意![]() ,都存在
,都存在![]() (
(![]() 為自然對數(shù)的底數(shù)),使得
為自然對數(shù)的底數(shù)),使得![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com