
點P是圓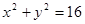 上的一個動點,過點P作PD垂直于
上的一個動點,過點P作PD垂直于 軸,垂足為D,Q為線段PD的中點。
軸,垂足為D,Q為線段PD的中點。
(1)求點Q的軌跡方程。
(2)已知點M(1,1)為上述所求方程的圖形內一點,過點M作弦AB,若點M恰為弦AB的中點,求直線AB的方程。
(1)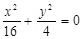 ;(2)
;(2)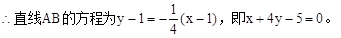
【解析】
試題分析:(Ⅰ)設Q(x,y),P(x0,y0),則D(x0,0),由Q為線段PD的中點,知x0=x, y0=2y,由P(x0,y0)在圓x2+y2=16上,知x02+y02=16,由此能求出點Q的軌跡方程.
(Ⅱ)設直線AB的方程為y-1=k(x-1).由y=k(x-1)+1 ,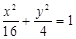 ,得(1+4k2)x+8k(1-k)x+4(1-k)2-16=0,設A(x1,y1),B(x2,y2),x1+x2=
,得(1+4k2)x+8k(1-k)x+4(1-k)2-16=0,設A(x1,y1),B(x2,y2),x1+x2= 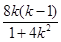 ,而M(1,1)是AB中點,則
,而M(1,1)是AB中點,則 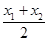 =1,由此能求出直線方程.
=1,由此能求出直線方程.
(1)設Q(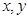 )
P(
)
P(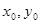 )
則D(
)
則D(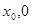 )
) 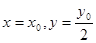 即
即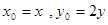
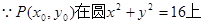
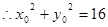
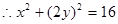 即
即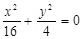 為所求。 …………4分
為所求。 …………4分
(2)法1:依題意顯然 的斜率存在,設直線AB的斜率為k,則AB的方程可設為
的斜率存在,設直線AB的斜率為k,則AB的方程可設為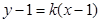 。
。
由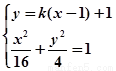 得
得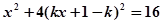
得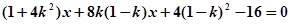 …………7分
…………7分
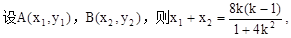
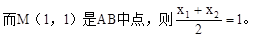
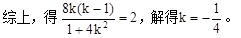 …………10分
…………10分
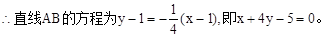 …………12分
…………12分
法2:(直接求k):設A(x1,y1),B(x2,y2)。
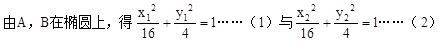
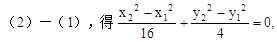 …………6分
…………6分
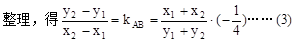 …………8分
…………8分
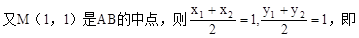
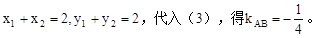 …………10分
…………10分
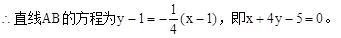 …………12分
…………12分
考點:本題主要考查了直線與圓錐曲線的綜合應用能力,具體涉及到軌跡方程的求法及直線與橢圓的相關知識,解題時要注意合理地進行等價轉化.
點評:解決該試題的關鍵是體現了解析幾何中設而不求的解題思想,聯立方程組,,轉化為二次方程的根的問題,結合韋達定理得到。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源:2011年湖北省武漢市武昌區高三元月調考數學試卷(理科)(解析版) 題型:選擇題
 上的一個動點,點Q是直線l:x-y=0上的一個動點,O為坐標原點,則向量
上的一個動點,點Q是直線l:x-y=0上的一個動點,O為坐標原點,則向量 上的投影的最大值是( )
上的投影的最大值是( )


查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com