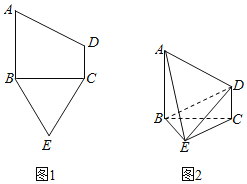
【題目】已知五邊形ABECD有一個直角梯形ABCD與一個等邊三角形BCE構成，如圖1所示，
，且
，將梯形ABCD沿著BC折起，形成如圖2所示的幾何體，且
平面BEC．
求證：平面
平面ADE；
求二面角
的平面角的余弦值．
科目：高中數學 來源： 題型：
【題目】某公司培訓員工某項技能，培訓有如下兩種方式：
方式一：周一到周五每天培訓1小時，周日測試
方式二：周六一天培訓4小時，周日測試
公司有多個班組，每個班組60人，現任選兩組
記為甲組、乙組
先培訓；甲組選方式一，乙組選方式二，并記錄每周培訓后測試達標的人數如表：
第一周 | 第二周 | 第三周 | 第四周 | |
甲組 | 20 | 25 | 10 | 5 |
乙組 | 8 | 16 | 20 | 16 |
用方式一與方式二進行培訓，分別估計員工受訓的平均時間精確到
，并據此判斷哪種培訓方式效率更高？
在甲乙兩組中，從第三周培訓后達標的員工中采用分層抽樣的方法抽取6人，再從這6人中隨機抽取2人，求這2人中至少有1人來自甲組的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知曲線
的方程為
．
（1）當
時，試確定曲線的形狀及其焦點坐標；
（2）若直線
交曲線于點
、
，線段
中點的橫坐標為
，試問此時曲線上是否存在不同的兩點
、
關于直線
對稱？
（3）當
為大于1的常數時，設
是曲線上的一點，過點
作一條斜率為
的直線，又設
為原點到直線的距離，
分別為點與曲線兩焦點的距離，求證
是一個定值，并求出該定值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司為了解共享單車的使用情況，隨機問卷50名使用者，然后根據這50名的問卷評分數據，統計得到如圖所示的頻率分布直方圖，其統計數據分組區間為[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]．
（1）求頻率分布直方圖中a的值；
（2）求這50名問卷評分數據的中位數；
（3）估計樣本的平均數．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】光線被曲線反射，等效于被曲線在反射點處的切線反射．已知光線從橢圓的一個焦點出發，被橢圓反射后要回到橢圓的另一個焦點；光線從雙曲線的一個焦點出發被雙曲線反射后的反射光線等效于從另一個焦點發出；如圖，橢圓
與雙曲線
（
，
）有公共焦點，現一光線從它們的左焦點出發，在橢圓與雙曲線間連續反射，則光線經過
次反射后，首次回到左焦點所經過的路徑長為______．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某快遞公司收取快遞費用的標準是：重量不超過
的包裹收費
元；重量超過的包裹，除收費元之外，超過的部分，每超出（不足時按計算）需再收
元．公司從承攬過的包裹中，隨機抽取
件，其重量統計如下：
公司又隨機抽取了
天的攬件數，得到頻數分布表如下：
以記錄的天的攬件數的頻率作為各攬件數發生的概率
計算該公司
天中恰有
天攬件數在
的概率；
估計該公司對每件包裹收取的快遞費的平均值；
公司將快遞費的三分之一作為前臺工作人員的工資和公司利潤，剩余的用做其他費用，目前前臺有工作人員人，每人每天攬件不超過
件，每人每天工資元，公司正在考慮是否將前臺工作人員裁減
人，試計算裁員前后公司每日利潤的數學期望，并判斷裁員是否對提高公司利潤有利？（同一組中的攬件數以這組數據所在區間中點值作代表）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】以下四個命題：
①“若
，則
”的逆否命題為真命題
②“
”是“函數
在區間
上為增函數”的充分不必要條件
③若
為假命題，則
，
均為假命題
④對于命題：
，
，則
為：
，
其中真命題的個數是（ ）
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】過拋物線外一點M作拋物線的兩條切線，兩切點的連線段稱為點M對應的切點弦已知拋物線為
，點P，Q在直線l：
上，過P，Q兩點對應的切點弦分別為AB，CD
當點P在l上移動時，直線AB是否經過某一定點，若有，請求出該定點的坐標；如果沒有，請說明理由
當
時，點P，Q在什么位置時，
取得最小值？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
