
【題目】已知函數![]()
![]() .
.
(1)若![]() ,判斷函數
,判斷函數![]() 的單調性;
的單調性;
(2)討論函數![]() 的極值,并說明理由.
的極值,并說明理由.
 步步高達標卷系列答案
步步高達標卷系列答案科目:高中數學 來源: 題型:
【題目】在統計學中,同比增長率一般是指和去年同期相比較的增長率,環比增長率一般是指和前一時期相比較的增長率.2020年2月29日人民網發布了我國2019年國民經濟和社會發展統計公報圖表,根據2019年居民消費價格月度漲跌幅度統計折線圖,下列說法正確的是( )
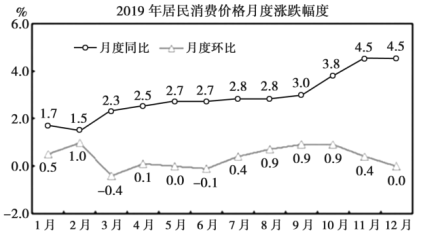
A.2019年我國居民每月消費價格與2018年同期相比有漲有跌
B.2019年我國居民每月消費價格中2月消費價格最高
C.2019年我國居民每月消費價格逐月遞增
D.2019年我國居民每月消費價格3月份較2月份有所下降
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以昆明、玉溪為中心的滇中地區,冬無嚴寒、夏無酷暑,世界上主要的鮮切花品種在這里都能實現周年規模化生產.某鮮花批發店每天早晨以每支2元的價格從鮮切花生產基地購入某種玫瑰,經過保鮮加工后全部裝箱(每箱500支,平均每支玫瑰的保鮮加工成本為1元),然后以每箱2000元的價格整箱出售.由于鮮花的保鮮特點,制定了如下促銷策略:若每天下午3點以前所購進的玫瑰沒有售完,則對未售出的玫瑰以每箱1200元的價格降價處理.根據經驗,降價后能夠把剩余玫瑰全部處理完畢,且當天不再購進該種玫瑰,由于庫房限制每天最多加工6箱.
(1)若某天該鮮花批發店購入并加工了6箱該種玫瑰,在下午3點以前售出4箱,且被6位不同的顧客購買.現從這6位顧客中隨機選取2人贈送優惠卡,則恰好一位是以2000元價格購買的顧客,另一位是以1200元價格購買的顧客的概率是多少?
(2)該鮮花批發店統計了100天內該種玫瑰在每天下午3點以前的銷售量![]() (單位:箱),統計結果如下表所示(視頻率為概率):
(單位:箱),統計結果如下表所示(視頻率為概率):
| 4 | 5 | 6 |
頻數 | 30 |
|
|
①估計接下來的一個月(30天)內該種玫瑰每天下午3點以前的銷售量不少于5箱的天數是多少?
②若批發店每天在購進5箱數量的玫瑰時所獲得的平均利潤最大(不考慮其他成本),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的一個頂點與拋物線
的一個頂點與拋物線![]() 的焦點重合,
的焦點重合,![]() ,
,![]() 分別是橢圓
分別是橢圓![]() 的左、右焦點,離心率
的左、右焦點,離心率![]() ,過橢圓
,過橢圓![]() 右焦點
右焦點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點.
兩點.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)是否存在直線![]() ,使得
,使得![]() ,若存在,求出直線
,若存在,求出直線![]() 的方程;若不存在,說明理由;
的方程;若不存在,說明理由;
(Ⅲ)設點![]() 是一個動點,若直線
是一個動點,若直線![]() 的斜率存在,且
的斜率存在,且![]() 為
為![]() 中點,
中點,![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近幾年來我國電子商務行業發展迅猛,2016年元旦期間,某購物平臺的銷售業績高達918億人民幣,與此同時,相關管理部門推出了針對電商的商品和服務的評價體系,現從評價系統中選出200次成功交易,并對其評價進行統計,對商品的好評率為0.6,對服務的好評率為0.75,其中對商品和服務都做出好評的交易為80次.
(1)完成商品和服務評價的![]() 列聯表,并說明是否可以在犯錯誤的概率不超過
列聯表,并說明是否可以在犯錯誤的概率不超過![]() 的前提下,認為商品好評與服務好評有關?
的前提下,認為商品好評與服務好評有關?
(2)若將頻率視為概率,某人在該購物平臺上進行的5次購物中,設對商品和服務全好評的次數為隨機變量![]() .
.
①求對商品和服務全好評的次數![]() 的分布列(概率用組合數算式表示);
的分布列(概率用組合數算式表示);
②求![]() 的數學期望和方差.
的數學期望和方差.
參考數據及公式如下:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(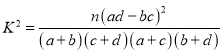 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),在同一平面直角坐標系中,將曲線
為參數),在同一平面直角坐標系中,將曲線![]() 上的點按坐標變換
上的點按坐標變換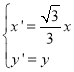 得到曲線
得到曲線![]() ,以原點為極點,
,以原點為極點,![]() 軸的正半軸為極軸,建立極坐標系.設
軸的正半軸為極軸,建立極坐標系.設![]() 點的極坐標為
點的極坐標為![]() .
.
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)若過點![]() 且傾斜角為
且傾斜角為![]() 的直線
的直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com