
【題目】在平面直角坐標(biāo)系![]() 中,已知橢圓
中,已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,且點
,且點![]() 與橢圓C的上頂點構(gòu)成邊長為2的等邊三角形.
與橢圓C的上頂點構(gòu)成邊長為2的等邊三角形.

(1)求橢圓C的方程;
(2)已知直線l與橢圓C相切于點P,且分別與直線![]() 和直線
和直線![]() 相交于點
相交于點![]() .試判斷
.試判斷![]() 是否為定值,并說明理由.
是否為定值,并說明理由.
【答案】(1)![]() (2)
(2)![]() 為定值
為定值![]() ;詳見解析
;詳見解析
【解析】
(1)根據(jù)題意可求得a,c的值,從而求得b,進(jìn)而得到橢圓方程;
(2)設(shè)直線l的方程為![]() ,聯(lián)立直線l與橢圓C的方程,根據(jù)直線與橢圓相切判別式為0得到關(guān)于k,m的關(guān)系式,聯(lián)立直線方程求出點M,N的坐標(biāo),由兩點的距離公式求出
,聯(lián)立直線l與橢圓C的方程,根據(jù)直線與橢圓相切判別式為0得到關(guān)于k,m的關(guān)系式,聯(lián)立直線方程求出點M,N的坐標(biāo),由兩點的距離公式求出![]() 、
、![]() ,從而通過化簡作商即可求出定值.
,從而通過化簡作商即可求出定值.
(1)依題意,![]() ,所以
,所以![]() ,所以橢圓C的標(biāo)準(zhǔn)方程為
,所以橢圓C的標(biāo)準(zhǔn)方程為![]() .
.
(2)因為直線l分別與直線![]() 和直線
和直線![]() 相交,所以直線l一定存在斜率.
相交,所以直線l一定存在斜率.
設(shè)直線![]() ,由
,由![]() 得
得![]() ,
,
由![]() ,得
,得![]() .①
.①
把![]() 代入
代入![]() ,得
,得![]() ,
,
把![]() 代入
代入![]() ,得
,得![]() ,
,
所以![]() ,
,![]() ,②
,②
由①式,得![]() ,③
,③
把③式代入②式,得![]() ,
,
所以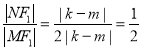 ,即
,即![]() 為定值
為定值![]() .
.


 提分百分百檢測卷單元期末測試卷系列答案
提分百分百檢測卷單元期末測試卷系列答案 小學(xué)期末標(biāo)準(zhǔn)試卷系列答案
小學(xué)期末標(biāo)準(zhǔn)試卷系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)求函數(shù)![]() 在區(qū)間[1,2]上的最大值;
在區(qū)間[1,2]上的最大值;
(2)設(shè)![]() 在(0,2)內(nèi)恰有兩個極值點,求實數(shù)m的取值范圍.
在(0,2)內(nèi)恰有兩個極值點,求實數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
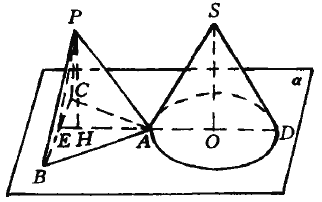
【題目】如圖,三棱錐![]() 的底面
的底面![]() 與圓錐
與圓錐![]() 的底面
的底面![]() 都在平面
都在平面![]() 上,且
上,且![]() 過點
過點![]() ,又
,又![]() 的直徑
的直徑![]() ,垂足為
,垂足為![]() .設(shè)三棱錐
.設(shè)三棱錐![]() 的所有棱長都是1,圓錐的底面直徑與母線長也都是1,圓錐的底面直徑與母線長也都是1.求圓錐的頂點
的所有棱長都是1,圓錐的底面直徑與母線長也都是1,圓錐的底面直徑與母線長也都是1.求圓錐的頂點![]() 到三棱錐
到三棱錐![]() 的三個側(cè)面的距離.
的三個側(cè)面的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)f(x)的定義域D={x|x≠0},且滿足對于任意x1,x2∈D.有f(x1·x2)=f(x1)+f(x2).
(1)求f(1)的值;
(2)判斷f(x)的奇偶性并證明;
(3)如果f(4)=1,f(3x+1)+f(2x-6)≤3,且f(x)在(0,+∞)上是增函數(shù),求x的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖是2020年2月1日到2月20日,某地區(qū)新型冠狀病毒疫情新增數(shù)據(jù)的走勢圖.
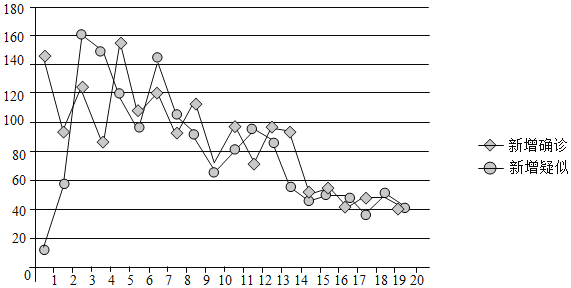
(Ⅰ)從這20天中任選1天,求新增確診和新增疑似的人數(shù)都超過100的概率;
(Ⅱ)從新增確診的人數(shù)超過100的日期中任選兩天,用X表示新增確診的人數(shù)超過140的天數(shù),求X的分布列和數(shù)學(xué)期望;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,函數(shù)g(x)=2﹣f(﹣x).
,函數(shù)g(x)=2﹣f(﹣x).
(1)判斷函數(shù)g(x)的奇偶性;
(2)若x∈(﹣1,0),
①求f(x)的值域;
②g(x)<tf(x)恒成立,求實數(shù)t的最大值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com