【題目】為了調查甲、乙兩種品牌商品的市場認可度，在某購物網點隨機選取了14天，統計在某確定時間段的銷量，得如下所示的統計圖，根據統計圖求：
（1）甲、乙兩種品牌商品銷量的中位數分別是多少？
（2）甲品牌商品銷量在[20，50]間的頻率是多少？
（3）甲、乙兩個品牌商品哪個更受歡迎？并說明理由.
【答案】(1) 甲、乙兩種品牌商品銷量的中位數分別是
；
（2）甲品牌商品銷量在
間的頻率
；
（3）甲品牌商品更受歡迎．
【解析】
試題分析：(1)利用莖葉圖能求出甲、乙兩種品牌商品銷量的中位數；
（2）甲品牌商品銷量在間的數據有
共5個，由此能求出甲品牌商品銷量在間的頻率.
(3)求出甲品牌商品的日平均銷售量和乙品牌商品的日平均銷售量，由此能求出結果.
試題解析：（1）甲的數據由小到大為：
乙的數據由小到大為：
所以甲、乙兩種品牌商品銷量的中位數分別是.
(2) 甲品牌商品銷量在間的數據有共5個，
所以甲品牌商品銷量在間的頻率.
(3) 解一：甲品牌商品的日平均銷售量為：
,
乙品牌商品的日平均銷售量為：
,
由
知甲品牌商品更受歡迎.
科目：高中數學 來源： 題型：
【題目】如圖，長方體ABCD﹣A1B1C1D1中，AB=16，BC=10，AA1=8，點E，F分別在A1B1，D1C1上，A1E=D1F=4，過點E，F的平面α與此長方體的面相交，交線圍成一個正方形．
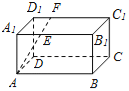
（1）在圖中畫出這個正方形（不必說明畫法和理由）；
（2）求直線AF與平面α所成角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=mlnx﹣x2+2（m∈R）．
（1）當m=1時，求f（x）的單調區間；
（2）若f（x）在x=1時取得極大值，求證：f（x）﹣f′（x）≤4x﹣3；
（3）若m≤8，當x≥1時，恒有f（x）﹣f′（x）≤4x﹣3恒成立，求m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知在三棱錐P﹣ABC中，PA⊥面ABC，AC⊥BC，且PA=AC=BC=1，點E是PC的中點，作EF⊥PB交PB于點F．
（Ⅰ）求證：PB⊥平面AEF；
（Ⅱ）求二面角A﹣PB﹣C的大小．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列說法中不正確的是（ ）
A. 對于線性回歸方程
，直線必經過點
B. 莖葉圖的優點在于它可以保存原始數據，并且可以隨時記錄
C. 將一組數據中的每一個數據都加上或減去同一常數后，方差恒不變
D. 擲一枚均勻硬幣出現正面向上的概率是
，那么一枚硬幣投擲2次一定出現正面
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】橢圓
的左右焦點分別為F1，F2，離心率為
，過點F1且垂直于x軸的直線被橢圓截得的弦長為
，直線l：y=kx+m與橢圓交于不同的A，B兩點．
（Ⅰ）求橢圓C的方程；
（Ⅱ）若在橢圓C上存在點Q滿足： 
（O為坐標原點）．求實數λ的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知f（x）=e2x+ln（x+a）．
（1）當a=1時，①求f（x）在（0，1）處的切線方程；②當x≥0時，求證：f（x）≥（x+1）2+x．
（2）若存在x0∈[0，+∞），使得 
成立，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知 
是函數f（x）=msinωx﹣cosωx（m＞0）的一條對稱軸，且f（x）的最小正周期為π
（Ⅰ）求m值和f（x）的單調遞增區間；
（Ⅱ）設角A，B，C為△ABC的三個內角，對應邊分別為a，b，c，若f（B）=2， 
，求 
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】根據空氣質量指數API（為整數）的不同，可將空氣質量分級如下表：
現對某城市30天的空氣質量進行監測，獲得30個API數據（每個數據均不同），統計繪得頻率分布直方圖如圖.
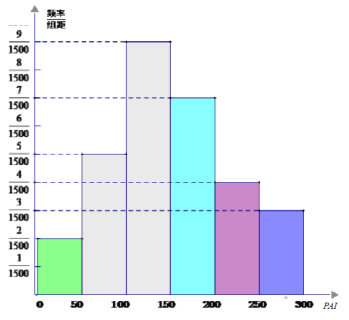
（1）請由頻率分布直方圖來估計這30天API 的平均值；
（2）若從獲得的“空氣質量優”和“空氣質量中重度污染” 的數據中隨機選取
個數據進行復查，求“空氣質量優”和“空氣質量中重度污染”數據恰均被選中的概率；
（3）假如企業每天由空氣污染造成的經濟損失S（單位：元）與空氣質量指數API （記為
）的關系式為
，
若將頻率視為概率，在本年內隨機抽取一天，試估計這天的經濟損失S不超過600元的概率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com