
【題目】如圖,在四棱錐![]() 中,已知棱
中,已知棱![]() ,
,![]() ,
,![]() 兩兩垂直,長度分別為1,2,2.若
兩兩垂直,長度分別為1,2,2.若![]() (
(![]() ),且向量
),且向量![]() 與
與![]() 夾角的余弦值為
夾角的余弦值為![]() .
.
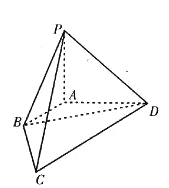
(1)求![]() 的值;
的值;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
試題(1)以![]() 為坐標原點,
為坐標原點,![]() 、
、![]() 、
、![]() 分別為
分別為![]() 、
、![]() 、
、![]() 軸建立空間直角坐標系
軸建立空間直角坐標系![]() ,寫出
,寫出![]() ,
,![]() 的坐標,根據空間向量夾角余弦公式列出關于
的坐標,根據空間向量夾角余弦公式列出關于![]() 的方程可求;(2)設岀平面
的方程可求;(2)設岀平面![]() 的法向量為
的法向量為![]() ,根據
,根據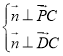 ,進而得到
,進而得到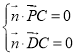 ,從而求出
,從而求出![]() ,向量
,向量![]() 的坐標可以求出,從而可根據向量夾角余弦的公式求出
的坐標可以求出,從而可根據向量夾角余弦的公式求出![]() ,從而得
,從而得![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
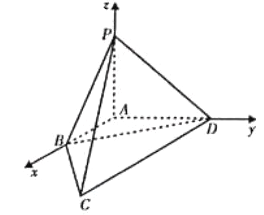
試題解析:(1)依題意,以![]() 為坐標原點,
為坐標原點,![]() 、
、![]() 、
、![]() 分別為
分別為![]() 、
、![]() 、
、![]() 軸建立空間直角坐標系
軸建立空間直角坐標系![]()
![]() ,因為
,因為![]() ,所以
,所以![]() ,從而
,從而![]() ,則由
,則由![]() ,解得
,解得![]() (舍去)或
(舍去)或![]() .
.
(2)易得![]() ,
,![]() ,設平面
,設平面![]() 的法向量
的法向量![]() ,
,
則![]() ,
,![]() ,即
,即![]() ,且
,且![]() ,所以
,所以![]() ,不妨取
,不妨取![]() ,則平面
,則平面![]() 的一個法向量
的一個法向量![]() ,又易得
,又易得![]() ,故
,故![]() ,所以直線
,所以直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.
考點: 1、空間兩向量夾角余弦公式;2、利用向量求直線和平面說成角的正弦.


 應用題天天練四川大學出版社系列答案
應用題天天練四川大學出版社系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,平面
中,平面![]() 平面ABCD,底面ABCD是直角梯形,
平面ABCD,底面ABCD是直角梯形,![]() ,
,![]() ,
,![]() .
.
(1)在線段PA上找一點E,使得![]() 平面PCD,并證明;
平面PCD,并證明;
(2)在(1)的條件下,若![]() ,求點E到平面PCD的距離.
,求點E到平面PCD的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了檢測某種零件的一條生產線的生產過程,從生產線上隨機抽取一批零件,根據其尺寸的數據分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 組,得到如圖所示的頻率分布直方圖.若尺寸落在區間
組,得到如圖所示的頻率分布直方圖.若尺寸落在區間![]() 之外,則認為該零件屬“不合格”的零件,其中
之外,則認為該零件屬“不合格”的零件,其中![]() ,
,![]() 分別為樣本平均和樣本標準差,計算可得
分別為樣本平均和樣本標準差,計算可得![]() (同一組中的數據用該組區間的中點值作代表).
(同一組中的數據用該組區間的中點值作代表).
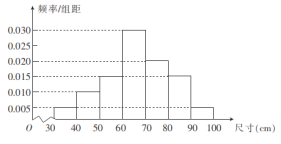
(1)若一個零件的尺寸是![]() ,試判斷該零件是否屬于“不合格”的零件;
,試判斷該零件是否屬于“不合格”的零件;
(2)工廠利用分層抽樣的方法從樣本的前![]() 組中抽出
組中抽出![]() 個零件,標上記號,并從這
個零件,標上記號,并從這![]() 個零件中再抽取
個零件中再抽取![]() 個,求再次抽取的
個,求再次抽取的![]() 個零件中恰有
個零件中恰有![]() 個尺寸小于
個尺寸小于![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】電視傳媒公司為了了解某地區電視觀眾對某類體育節目的收視情況,隨機抽取了100名觀眾進行調查,其中女性有55名.下面是根據調查結果繪制的觀眾日均收看該體育節目時間的頻率分布直方圖;
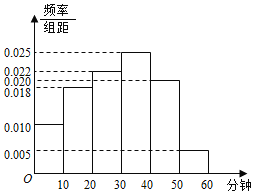
將日均收看該體育節目時間不低于40分鐘的觀眾稱為“體育迷”,已知“體育迷”中有10名女性.
非體育迷 | 體育迷 | 合計 | |
男 | |||
女 | |||
合計 |
(1)根據已知條件完成下面的![]() 列聯表,并據此資料你是否認為“體育迷”與性別有關?
列聯表,并據此資料你是否認為“體育迷”與性別有關?
(2)將日均收看該體育項目不低于50分鐘的觀眾稱為“超級體育迷”,已知“超級體育迷”中有2名女性,若從“超級體育迷”中任意選取2人,求至少有1名女性觀眾的概率.
附:參考公式:![]() .
.
| 0.05 | 0.01 |
| 3.841 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《數書九章》是中國南宋時期杰出數學家秦九韶的著作,全書十八卷共八十一個問題,分為九類,每類九個問題,《數書九章》中記錄了秦九昭的許多創造性成就,其中在卷五“三斜求積”中提出了已知三角形三邊![]() ,
,![]() ,
,![]() 求面積的公式,這與古希臘的海倫公式完成等價,其求法是:“以小斜冪并大斜冪減中斜冪,余半之,自乘于上,以小斜冪乘大斜冪減上,余四約之,為實,一為從隅,開平方得積.”若把以上這段文字寫成公式,即
求面積的公式,這與古希臘的海倫公式完成等價,其求法是:“以小斜冪并大斜冪減中斜冪,余半之,自乘于上,以小斜冪乘大斜冪減上,余四約之,為實,一為從隅,開平方得積.”若把以上這段文字寫成公式,即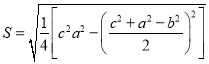 .現有
.現有![]() 滿足
滿足![]() ,且
,且![]() 的面積
的面積![]() ,請運用上述公式判斷下列命題正確的是
,請運用上述公式判斷下列命題正確的是
A.![]() 周長為
周長為![]()
B.![]() 三個內角
三個內角![]() ,
,![]() ,
,![]() 成等差數列
成等差數列
C.![]() 外接圓直徑為
外接圓直徑為![]()
D.![]() 中線
中線![]() 的長為
的長為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() ,AB的垂直平分線分別交AB,AC于D、E(圖一),沿DE將
,AB的垂直平分線分別交AB,AC于D、E(圖一),沿DE將![]() 折起,使得平面
折起,使得平面![]() 平面BDEC(圖二).
平面BDEC(圖二).

(1)若F是AB的中點,求證:![]() 平面ADE.
平面ADE.
(2)P是AC上任意一點,求證:平面![]() 平面PBE.
平面PBE.
(3)P是AC上一點,且![]() 平面PBE,求二面角
平面PBE,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知平面向量![]() 滿足
滿足![]() ,則以下說法正確的有( )個.
,則以下說法正確的有( )個.
①![]() ;
;
②對于平面內任一向量![]() ,有且只有一對實數
,有且只有一對實數![]() ,
,![]() 使
使![]() ;
;
③若![]() ,且
,且![]() ,則
,則![]() 的范圍為
的范圍為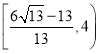 ;
;
④設![]() ,且
,且![]() 在
在![]() 處取得最小值,當
處取得最小值,當![]() 時,則
時,則![]() ;
;
A.1B.2C.3D.4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com