
【題目】在![]() 中,
中,![]() ,
,![]() ,AB的垂直平分線分別交AB,AC于D、E(圖一),沿DE將
,AB的垂直平分線分別交AB,AC于D、E(圖一),沿DE將![]() 折起,使得平面
折起,使得平面![]() 平面BDEC(圖二).
平面BDEC(圖二).

(1)若F是AB的中點,求證:![]() 平面ADE.
平面ADE.
(2)P是AC上任意一點,求證:平面![]() 平面PBE.
平面PBE.
(3)P是AC上一點,且![]() 平面PBE,求二面角
平面PBE,求二面角![]() 的大小.
的大小.
【答案】(1)見解析(2)見解析(3)![]()
【解析】
(1)取BD的中點為M,連續FM,CM,通過證明面![]() 面ADE,由此證得
面ADE,由此證得![]() 面ADE;(2)由平面幾何知識可知
面ADE;(2)由平面幾何知識可知![]() ,
,![]() ,平面
,平面![]() 平面BDEC,則
平面BDEC,則![]() 平面BDEC,從而
平面BDEC,從而![]() ,根據線面垂直的判定定理可知
,根據線面垂直的判定定理可知![]() 面ACD,而
面ACD,而![]() 面PBE,最后根據面面垂直的判定定理可知平面
面PBE,最后根據面面垂直的判定定理可知平面![]() 平面PBE;
平面PBE;
(3)根據(2)![]() 面ACD,設
面ACD,設![]() ,則
,則![]() ,
,![]() ,根據二面角平面角的定義可知
,根據二面角平面角的定義可知![]() 為二面角
為二面角![]() 的平面角,在三角形PQC中求出此角即可.
的平面角,在三角形PQC中求出此角即可.
(1)證明:取BD的中點為M,連續FM,CM
![]() 為AB的中點,
為AB的中點,![]() ,
,
由題知![]() 為等邊三角形,
為等邊三角形,![]() ,又
,又![]()
![]() ,∴面
,∴面![]() 面ADE,
面ADE,![]() 面CMF,
面CMF,![]() 面ADE
面ADE
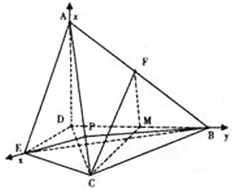
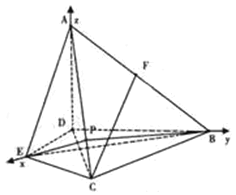
圖1 圖2
(2)證明:由平面幾何知識:![]() ,
,![]() ,平面
,平面![]() 平面BDEC
平面BDEC
![]() 平面BDEC,
平面BDEC,![]() ,
,![]() 面ACD,
面ACD,![]() 面PBE,
面PBE,
∴平面![]() 平面PBE
平面PBE
(3)由(2)![]() 面ACD,
面ACD,
設![]() ,
,
由題意知![]() ,
,![]() ,
,
![]() 為二面角
為二面角![]() 的平面角
的平面角
![]() ,
,![]() ,
,![]() ,
,![]()
∴二面角![]() 的大小為
的大小為![]()


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】隨著經濟水平及個人消費能力的提升,我國居民對精神層面的追求愈加迫切,如圖是2007年到2017年我國城鎮居民教育、文化、服務人均消費支出同比增速的折線圖,圖中顯示2007年的同比增速為10%, 即2007年與2006年同時期比較2007年的人均消費支出費用是2006年的1.1倍.則下列表述中正確的是( )
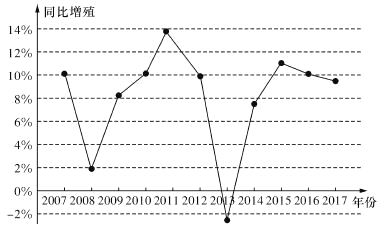
A.2007年到2017年,同比增速的中位數約為10%
B.2007年到2017年,同比增速的極差約為12%
C.2011年我國城鎮居民教育、文化、服務人均消費支出的費用最高
D.2007年到2017年,我國城鎮居民教育、文化、服務人均消費支出的費用逐年增加
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,已知棱
中,已知棱![]() ,
,![]() ,
,![]() 兩兩垂直,長度分別為1,2,2.若
兩兩垂直,長度分別為1,2,2.若![]() (
(![]() ),且向量
),且向量![]() 與
與![]() 夾角的余弦值為
夾角的余弦值為![]() .
.
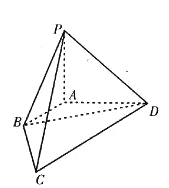
(1)求![]() 的值;
的值;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】直線![]() ax+by=1與圓x2+y2=1相交于A,B兩點(其中a,b是實數),且△AOB是直角三角形(O是坐標原點),則點P(a,b)與點(0,1)之間距離的最小值為( ).
ax+by=1與圓x2+y2=1相交于A,B兩點(其中a,b是實數),且△AOB是直角三角形(O是坐標原點),則點P(a,b)與點(0,1)之間距離的最小值為( ).
A.0B.![]() C.
C.![]() -1D.
-1D.![]() +1
+1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的一個焦點為
的一個焦點為![]() ,且
,且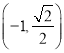 在橢圓E上.
在橢圓E上.
(1)求橢圓E的標準方程;
(2)已知垂直于x軸的直線![]() 交E于A、B兩點,垂直于y軸的直線
交E于A、B兩點,垂直于y軸的直線![]() 交E于C、D兩點,
交E于C、D兩點,![]() 與
與![]() 的交點為P,且
的交點為P,且![]() ,間:是否存在兩定點M,N,使得
,間:是否存在兩定點M,N,使得![]() 為定值?若存在,求出M,N的坐標,若不存在,請說明理由.
為定值?若存在,求出M,N的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《宋人撲棗圖軸》是作于宋朝的中國古畫,現收藏于中國臺北故宮博物院.該作品簡介:院角的棗樹結實累累,小孩群來攀扯,枝椏不停晃動,粒粒棗子搖落滿地,有的牽起衣角,有的捧著盤子拾取,又玩又吃,一片興高采烈之情,躍然于絹素之上.甲、乙、丙、丁四人想根據該圖編排一個舞蹈,舞蹈中他們要模仿該圖中小孩撲棗的爬、扶、撿、頂四個動作,四人每人模仿一個動作.若他們采用抽簽的方式來決定誰模仿哪個動作,則甲不模仿“爬”且乙不模仿“扶”的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com