
【題目】已知數列![]() 的前
的前![]() 項和為
項和為![]() ,并且滿足
,并且滿足![]() ,
, ![]() .
.
(1)求數列![]() 通項公式;
通項公式;
(2)設![]() 為數列
為數列![]() 的前
的前![]() 項和,求證:
項和,求證: ![]() .
.
【答案】(1) ![]() (2)見解析
(2)見解析
【解析】試題分析:(1)根據題意得到![]() ,
, ![]() ,兩式做差得到
,兩式做差得到![]() ;(2)根據第一問得到
;(2)根據第一問得到![]() ,由錯位相減法得到前n項和,進而可證和小于1.
,由錯位相減法得到前n項和,進而可證和小于1.
解析:
(1)∵![]()
當![]() 時,
時, ![]()
當![]() 時,
時, ![]() ,即
,即![]()
∴數列![]() 時以
時以![]() 為首項,
為首項, ![]() 為公差的等差數列.
為公差的等差數列.
∴![]() .
.
(2)∵![]()
∴![]() ①
①
![]() ②
②
由①![]() ②得
②得
![]()
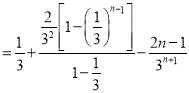
![]()
∴![]()
點睛:這個題目考查的是數列通項公式的求法及數列求和的常用方法;數列通項的求法中有常見的已知![]() 和
和![]() 的關系,求
的關系,求![]() 表達式,一般是寫出
表達式,一般是寫出![]() 做差得通項,但是這種方法需要檢驗n=1時通項公式是否適用;數列求和常用法有:錯位相減,裂項求和,分組求和等.
做差得通項,但是這種方法需要檢驗n=1時通項公式是否適用;數列求和常用法有:錯位相減,裂項求和,分組求和等.
【題型】解答題
【結束】
22
【題目】已知![]() ,
, ![]() 分別是橢圓
分別是橢圓![]() :
: ![]() (
(![]() )的左、右焦點,
)的左、右焦點, ![]() 是橢圓
是橢圓![]() 上的一點,且
上的一點,且![]() ,橢圓
,橢圓![]() 的離心率為
的離心率為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若直線![]() :
: ![]() 與橢圓
與橢圓![]() 交于不同兩點
交于不同兩點![]() ,
, ![]() ,橢圓
,橢圓![]() 上存在點
上存在點![]() ,使得以
,使得以![]() ,
, ![]() 為鄰邊的四邊形
為鄰邊的四邊形![]() 為平行四邊形(
為平行四邊形(![]() 為坐標原點).
為坐標原點).
(ⅰ)求實數![]() 與
與![]() 的關系;
的關系;
(ⅱ)證明:四邊形![]() 的面積為定值.
的面積為定值.
【答案】(1) ![]() (2)①
(2)①![]() ② 四邊形
② 四邊形![]() 的面積為定值,且定值為
的面積為定值,且定值為![]()
【解析】試題分析:(1)根據題意得到![]() ,
, ![]() ,橢圓的標準方程為
,橢圓的標準方程為![]() ;(2)聯立直線和橢圓方程得到二次方程,根據題意得到
;(2)聯立直線和橢圓方程得到二次方程,根據題意得到![]() ,由韋達定理得到P點坐標,再根據點在橢圓上得到參數值關系;(3)先由弦長公式得到
,由韋達定理得到P點坐標,再根據點在橢圓上得到參數值關系;(3)先由弦長公式得到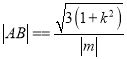 ,由點線距得到三角形高度,再根據四邊形面積公式
,由點線距得到三角形高度,再根據四邊形面積公式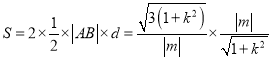 ,進而得到定值.
,進而得到定值.
解析:
(1)依題意, ![]() ,即
,即![]() .
.
又![]() ,∴
,∴![]()
∴![]()
故橢圓的標準方程為![]()
(2)(ⅰ)由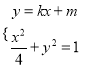 消
消![]() 得
得![]() .
.
則![]()
設![]() ,
, ![]() ,則
,則![]() ,
, ![]() .
.
∴![]()
∵四邊形![]() 為平行四邊形.
為平行四邊形.
∴![]()
![]()
∴點![]() 坐標為
坐標為![]()
∵點![]() 在橢圓
在橢圓![]() 上,
上,
∴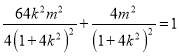 ,整理得
,整理得![]()
(ⅱ)∵![]()
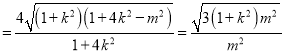
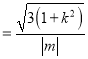
又點![]() 到直線
到直線![]() :
: ![]() 的距離為
的距離為![]()
∴四邊形![]() 的面積
的面積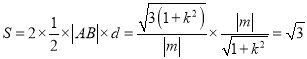
故四邊形![]() 的面積為定值,且定值為
的面積為定值,且定值為![]() .
.


 快樂暑假暑假能力自測中西書局系列答案
快樂暑假暑假能力自測中西書局系列答案科目:高中數學 來源: 題型:
【題目】如圖所示,已知AB為圓O的直徑,C,D是圓O上的兩個點,CE⊥AB于E,BD交AC于G,交CE于F,CF=FG. 
(1)求證:AC是∠DAB的平分線;
(2)求證:OF∥AG.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某家庭進行理財投資,有兩種方式,甲為投資債券等穩健型產品,乙為投資股票等風險型產品,設投資甲、乙兩種產品的年收益分別為![]() 、
、![]() 萬元,根據長期收益率市場預測,它們與投入資金
萬元,根據長期收益率市場預測,它們與投入資金![]() 萬元的關系分別為
萬元的關系分別為![]() ,
,![]() ,(其中
,(其中![]() ,
,![]() ,
,![]() 都為常數),函數
都為常數),函數![]() ,
,![]() 對應的曲線
對應的曲線![]() ,
,![]() 如圖所示.
如圖所示.
(1)求函數![]() 、
、![]() 的解析式;
的解析式;
(2)若該家庭現有![]() 萬元資金,全部用于理財投資,問:如何分配資金能使一年的投資獲得最大收益,其最大收益是多少萬元?
萬元資金,全部用于理財投資,問:如何分配資金能使一年的投資獲得最大收益,其最大收益是多少萬元?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】拋物線![]() (
(![]() )的焦點為
)的焦點為![]() ,已知點
,已知點![]() ,
, ![]() 為拋物線上的兩個動點,且滿足
為拋物線上的兩個動點,且滿足![]() .過弦
.過弦![]() 的中點
的中點![]() 作拋物線準線的垂線
作拋物線準線的垂線![]() ,垂足為
,垂足為![]() ,則
,則![]() 的最大值為__________.
的最大值為__________.
【答案】1
【解析】設![]() ,在三角形ABF中,用余弦定理得到
,在三角形ABF中,用余弦定理得到![]()
![]() ,
, 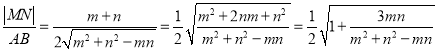
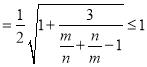 故最大值為1.
故最大值為1.
故答案為:1.
點睛:本題主要考查了拋物線的簡單性質.解題的關鍵是利用了拋物線的定義。一般和拋物線有關的小題,很多時可以應用結論來處理的;平時練習時應多注意拋物線的結論的總結和應用。尤其和焦半徑聯系的題目,一般都和定義有關,實現點點距和點線距的轉化。
【題型】填空題
【結束】
17
【題目】設![]() 的內角
的內角![]() ,
, ![]() ,
, ![]() 所對的邊分別為
所對的邊分別為![]() ,
, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() .
.
(1)當![]() 時,求
時,求![]() 的值;
的值;
(2)當![]() 的面積為
的面積為![]() 時,求
時,求![]() 的周長.
的周長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形ABCD內接于⊙O,過點A作⊙O的切線EP交CB的延長線于P,∠PAB=35°. 
(1)若BC是⊙O的直徑,求∠D的大小;
(2)若∠PAB=35°,求證: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() ,半徑為2的圓
,半徑為2的圓![]() 與
與![]() 相切,圓心
相切,圓心![]() 在
在![]() 軸上且在直線
軸上且在直線![]() 的上方.
的上方.
(1)求圓![]() 的方程;
的方程;
(2)過點![]() 的直線與圓
的直線與圓![]() 交于
交于![]() 兩點(
兩點(![]() 在
在![]() 軸上方),問在
軸上方),問在![]() 軸正半軸上是否存在定點
軸正半軸上是否存在定點![]() ,使得
,使得![]() 軸平分
軸平分![]() ?若存在,求出點
?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為奇函數,
為奇函數,![]() 為偶函數,且
為偶函數,且![]() .
.
(Ⅰ)求函數![]() 及
及![]() 的解析式;
的解析式;
(Ⅱ)用函數單調性的定義證明:函數![]() 在
在![]() 上是減函數;
上是減函數;
(Ⅲ)若關于![]() 的方程
的方程![]() 有解,求實數
有解,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,PA⊥底面ABCD,AC⊥AB,AD⊥DC,∠DAC=60°,PA=AC=2,AB=1. 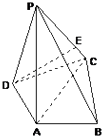
(1)求二面角A﹣PB﹣C的余弦值.
(2)在線段CP上是否存在一點E,使得DE⊥PB,若存在,求線段CE的長度,不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com