
【題目】已知![]() .
.
(1)證明![]() 在
在![]() 上為增函數(shù);
上為增函數(shù);
(2)當![]() 時,解不等式
時,解不等式![]() ;
;
(3)若![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的最大整數(shù)值.
的最大整數(shù)值.
【答案】(1)見解析(2)![]() (3)0
(3)0
【解析】試題分析:
(1)首先求得函數(shù)的導(dǎo)函數(shù),然后對![]() 進行二次求導(dǎo)可得
進行二次求導(dǎo)可得![]() 在
在![]() 上為增函數(shù);
上為增函數(shù);
(2)利用(1)中函數(shù)的單調(diào)性結(jié)合題意可得不等式的解集為![]()
(3)不等式即![]() ,構(gòu)造新函數(shù)
,構(gòu)造新函數(shù)![]() ,結(jié)合導(dǎo)函數(shù)的性質(zhì)可得
,結(jié)合導(dǎo)函數(shù)的性質(zhì)可得![]() 的最大整數(shù)值為0.
的最大整數(shù)值為0.
試題解析:
解:(1)![]() ,設(shè)
,設(shè)![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
|
|
|
|
| - | 0 | + |
| ↓ | 極小值 | ↑ |
![]()
![]()
![]() ,
,
![]()
![]() ,
, ![]()
![]() ,
,
![]()
![]() 在
在![]() 上為增函數(shù).
上為增函數(shù).
(2)![]() 時,
時, ![]() ,
, ![]()
![]() 在
在![]() 上為增函數(shù),
上為增函數(shù),
![]() 若
若![]() ,則
,則![]() ,與
,與![]() 矛盾;
矛盾;
若![]() ,則
,則![]() ,
, ![]() 成立.
成立.
經(jīng)化簡![]() ,則
,則![]() ,
, ![]()
![]() ,即
,即![]() ,
,
![]()
![]() ,即
,即![]() ,
,
![]() 設(shè)
設(shè)![]() ,
,
![]()
![]() ,
,
![]()
![]() 在
在![]() 上為增函數(shù),
上為增函數(shù), ![]()
![]() ,得
,得![]() ,
,
![]() 原不等式解集為
原不等式解集為![]() .
.
(3)![]()
![]() 在
在![]() 上為增函數(shù),
上為增函數(shù), ![]()
![]() ,即
,即![]() ,令
,令
![]() ,
, ![]()
![]() ,
,
設(shè)![]() ,
, ![]() ,
,
![]()
![]() 時,
時, ![]() ,
, ![]() ,
,
![]()
![]() 在
在![]() 為增函數(shù),
為增函數(shù),
![]()
![]() 在
在![]() 為增函數(shù),
為增函數(shù),
![]() ,
, 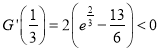 ,
,
![]()
![]() 有任一解,設(shè)為
有任一解,設(shè)為![]() ,
,
![]()
![]() 時,
時,
|
|
|
|
| - | 0 | + |
| ↓ | 極 | ↑ |
![]()
![]()
![]() ,
,
![]()
![]() 即
即![]() ,
,
![]()
![]()
![]() ,
,
又![]()
![]() ,
, ![]()
![]() .
.


 名校名師培優(yōu)作業(yè)本加核心試卷系列答案
名校名師培優(yōu)作業(yè)本加核心試卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中點. 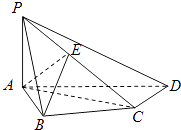
(1)證明CD⊥AE;
(2)證明PD⊥平面ABE;
(3)求二面角A﹣PD﹣C的正切值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=(ex+1)(ax+2a﹣2),若存在x∈(0,+∞),使得不等式f(x)﹣2<0成立,則實數(shù)a的取值范圍是( )
A.(0,1)
B.(0, ![]() )
)
C.(﹣∞,1)
D.(﹣∞, ![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,曲線c1:y2=2px(p>0)與曲線c2:(x﹣6)2+y2=36只有三個公共點O,M,N,其中O為坐標原點,且 ![]() =0.
=0. 
(1)求曲線c1的方程;
(2)過定點M(3,2)的直線l與曲線c1交于A,B兩點,若點M是線段AB的中點,求線段AB的長.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知A={x| ![]() <3x<9},B={x|log2x>0}.
<3x<9},B={x|log2x>0}.
(1)求A∩B和A∪B;
(2)定義A﹣B={x|x∈A且xB},求A﹣B和B﹣A.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四面體ABCD中,O、E分別是BD、BC的中點,CA=CB=CD=BD=2,AB=AD= ![]() .
.
(Ⅰ)求證:AO⊥平面BCD;
(Ⅱ)求異面直線AB與CD所成角的余弦;
(Ⅲ)求點E到平面ACD的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知等差數(shù)列{an}滿足an+1>an , a1=1,且該數(shù)列的前三項分別加上1,1,3后順次成為等比數(shù)列{bn}的前三項.
(1)求數(shù)列{an},{bn}的通項公式;
(2)令cn=anbn , 求數(shù)列{cn}的前n項和Sn .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】知函數(shù)f(x)= ![]() (a>1),求:
(a>1),求:
(1)判斷函數(shù)的奇偶性;
(2)證明f(x)是R上的增函數(shù);
(3)求該函數(shù)的值域.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校為了解高一學(xué)生周末的“閱讀時間”,從高一年級中隨機抽取了![]() 名學(xué)生進行調(diào)査,獲得了每人的周末“閱讀時間”(單位:小時),按照
名學(xué)生進行調(diào)査,獲得了每人的周末“閱讀時間”(單位:小時),按照![]() 分成
分成![]() 組,制成樣本的頻率分布直方圖如圖所示:
組,制成樣本的頻率分布直方圖如圖所示:
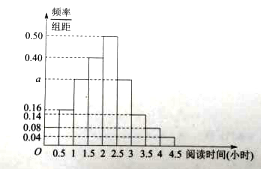
(Ⅰ)求圖中![]() 的值;
的值;
(Ⅱ)估計該校高一學(xué)生周末“閱讀時間”的中位數(shù);
(Ⅲ)用樣本頻率代替概率. 現(xiàn)從全校高一年級隨機抽取![]() 名學(xué)生,其中有
名學(xué)生,其中有![]() 名學(xué)生“閱讀時間”在
名學(xué)生“閱讀時間”在![]() 小時內(nèi)的概率為
小時內(nèi)的概率為![]() ,其中
,其中![]() .當
.當![]() 取最大時,求
取最大時,求![]() 的值.
的值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com