【題目】黃岡“一票通”景區旅游年卡，是由黃岡市旅游局策劃，黃岡市大別山旅游公司推出的一項惠民工程.持有旅游年卡一年內可不限次暢游全市19家簽約景區.為合理配置旅游資源，現對已游覽某簽約景區的游客進行滿意度調查.隨機抽取100位游客進行調查評分（滿分100分），評分的頻率分布直方圖如圖.
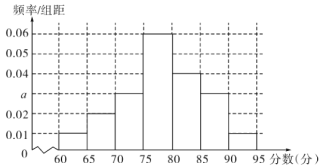
（1）求a的值并估計評分的平均數；
（2）為了了解游客心聲，調研機構用分層抽樣的方法從評分為
，
的游客中抽取了6名，聽取他們對該景區建設的建議.現從這6名游客中選取2人，求這2人中至少有一個人的評分在內的概率；
（3）為更廣泛了解游客想法，調研機構對所有評分從低到高排序的前86%游客進行了網上問卷調查并隨調查表贈送小禮品，估計收到問卷調查表的游客的最高分數.
【答案】（1）
，
；（2）
；（3）
【解析】
（1）根據頻率和為1即可求得a的值;根據平均數的求法,代入即可求得評分的平均數.
（2）在
,
的游客中抽取了6名,其中在抽取2人,在中抽取4人,根據古典概型概率求法,列舉出所有可能,即可求得至少有一個人的評分在內的概率.
（3）先求得從低分到高分排列, 最低的前86%最高分落在的評分區間,利用百分比即可求得最高分.
（1）由
,得.
游客評分的平均數為：
（2）抽取的6名游客,評分在
內的4個,記為1,2,3,4,
在
內的2個,記為5,6
從這6人隨機選取2人,有12,13,14,15,16,23,24,25,26,34,35,36,45,35,56共15中選法,其中至少有一個在內有15,16,25,26,35,36,45,46,56共9種
由古典概型,
.
（3）評分低于85分的概率為
故評分最低的前86%最高分在
設最高分為x,由
得
科目：高中數學 來源： 題型：
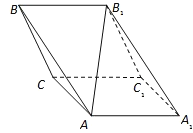
【題目】斜三棱柱ABC﹣A1B1C1，已知側面BB1C1C與底面ABC垂直且∠BCA=90°，∠B1BC=60°，BC=BB1=2，若二面角A﹣B1B﹣C為30°
（1）求AB1與平面BB1C1C所成角的正切值；
（2）在平面AA1B1B內找一點P，使三棱錐P﹣BB1C為正三棱錐，并求P到平面BB1C距離.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已過拋物線
：
的焦點
作直線
交拋物線于
，
兩點，以，兩點為切點作拋物線的切線，兩條直線交于
點.
（1）當直線平行于
軸時，求點的坐標；
（2）當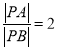
時，求直線的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線
的焦點為橢圓
的右焦點，且橢圓長軸的長為4，
、
是橢圓上的兩點；
（1）求橢圓標準方程；
（2）若直線
經過點
，且
，求直線的方程；
（3）若動點
滿足：
，直線
與
的斜率之積為
，是否存在兩個定點
、
，使得
為定值？若存在，求出、的坐標；若不存在，請說明理由；
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設橢圓C的方程為
，O為坐標原點，A為橢團的上頂點，
為其右焦點，D是線段
的中點，且
.
（1）求橢圓C的方程；
（2）過坐標原點且斜率為正數的直線交橢圓C于P，Q兩點，分別作
軸，
軸，垂足分別為E，F，連接
，
并延長交橢圓C于點M，N兩點.
（ⅰ）判斷
的形狀；
（ⅱ）求四邊形
面積的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列
是公差
的等差數列，且
．
（1）求的前
項的和
；
（2）若
，問在數列中是否存在一項
（
是正整數），使得
成等比數列，若存在，求出的值，若不存在，請說明理由；
（3）若存在自然數
（
是正整數），滿足
，使得
成等比數列，求所有整數
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知集合
，且
中的元素個數
大于等于5.若集合中存在四個不同的元素
，使得
，則稱集合是“關聯的”，并稱集合
是集合的“關聯子集”；若集合不存在“關聯子集”，則稱集合是“獨立的”.
分別判斷集合
和集合
是“關聯的”還是“獨立的”？若是“關聯的”，寫出其所有的關聯子集；
已知集合
是“關聯的”，且任取集合
，總存在的關聯子集
，使得
.若
，求證：
是等差數列；
集合是“獨立的”，求證：存在
，使得
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
