
【題目】如圖,在四棱錐P﹣ABCD中,四邊形ABCD為平行四邊形,AC,BD相交于點O,點E為PC的中點,OP=OC,PA⊥PD.求證: 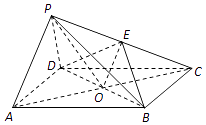
(1)直線PA∥平面BDE;
(2)平面BDE⊥平面PCD.
【答案】
(1)證明:連結OE,因為O為平行四邊形ABCD對角線的交點,所以O為AC中點.
又因為E為PC的中點,
所以OE∥PA.
又因為OE平面BDE,PA平面BDE,
所以直線PA∥平面BDE
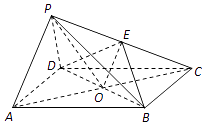
(2)證明:因為OE∥PA,PA⊥PD,所以OE⊥PD.
因為OP=OC,E為PC的中點,所以OE⊥PC.
又因為PD平面PCD,PC平面PCD,PC∩PD=P,
所以OE⊥平面PCD.
又因為OE平面BDE,所以平面BDE⊥平面PCD..
【解析】(1)連結OE,說明OE∥PA.然后證明PA∥平面BDE.(2)證明OE⊥PD.OE⊥PC.推出OE⊥平面PCD.然后證明平面BDE⊥平面PCD.
【考點精析】本題主要考查了直線與平面平行的判定和平面與平面垂直的判定的相關知識點,需要掌握平面外一條直線與此平面內的一條直線平行,則該直線與此平面平行;簡記為:線線平行,則線面平行;一個平面過另一個平面的垂線,則這兩個平面垂直才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】為調查乘客的候車情況,公交公司在某為臺的![]() 名候車乘客中隨機抽取
名候車乘客中隨機抽取![]() 人,將他們的候車時間(單位:分鐘)作為樣本分成
人,將他們的候車時間(單位:分鐘)作為樣本分成![]() 組,如下表所示:
組,如下表所示:
組別 | 候車時間 | 人數 |
一 |
|
|
二 |
|
|
三 |
|
|
四 |
|
|
五 |
|
|
(1)求這![]() 名乘客的平均候車時間;
名乘客的平均候車時間;
(2)估計這![]() 名候車乘客中候車時間少于
名候車乘客中候車時間少于![]() 分鐘的人數;
分鐘的人數;
(3)若從上表第三、四組的![]() 人中隨機抽取
人中隨機抽取![]() 人作進一步的問卷調查,求抽到的兩人恰好來自不同組的概率.
人作進一步的問卷調查,求抽到的兩人恰好來自不同組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某小區內有兩條互相垂直的道路![]() 與
與![]() ,分別以
,分別以![]() 、
、![]() 所在直線為
所在直線為![]() 軸、
軸、![]() 軸建立如圖所示的平面直角坐標系
軸建立如圖所示的平面直角坐標系![]() ,其第一象限有一塊空地
,其第一象限有一塊空地![]() ,其邊界
,其邊界![]() 是函數
是函數![]() 的圖象,前一段曲線
的圖象,前一段曲線![]() 是函數
是函數![]() 圖象的一部分,后一段
圖象的一部分,后一段![]() 是一條線段.測得
是一條線段.測得![]() 到
到![]() 的距離為
的距離為![]() 米,到
米,到![]() 的距離為
的距離為![]() 米,
米,![]() 長為
長為![]() 米.現要在此地建一個社區活動中心,平面圖為梯形
米.現要在此地建一個社區活動中心,平面圖為梯形![]() (其中點
(其中點![]() 在曲線
在曲線![]() 上,點
上,點![]() 在線段
在線段![]() 上,且
上,且![]() 、
、![]() 為兩底邊).
為兩底邊).
(1)求函數![]() 的解析式;
的解析式;
(2)當梯形的高為多少米時,該社區活動中心的占地面積最大,并求出最大面積.

查看答案和解析>>
科目:高中數學 來源: 題型:
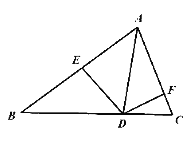
【題目】在銳角![]() 中,已知
中,已知![]() ,
,![]() ,若點
,若點![]() 是線段
是線段![]() 上一點(不含端點),過
上一點(不含端點),過![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() .
.
(1)若![]() 外接圓的直徑長為
外接圓的直徑長為![]() ,求
,求![]() 的值;
的值;
(2)求![]() 的最小值
的最小值
(3)問點![]() 在何處時,
在何處時,![]() 的面積最大?最大值為多少?
的面積最大?最大值為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校將從4名男生和4名女生中選出4人分別擔任辯論賽中的一、二、三、四辯手,其中男生甲不適合擔任一辯手,女生乙不適合擔任四辯手.現要求:如果男生甲入選,則女生乙必須入選.那么不同的組隊形式有_________種.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ln(a x)+bx在點(1,f(1))處的切線是y=0;
(I)求函數f(x)的極值;
(II)當![]() 恒成立時,求實數m的取值范圍(e為自然對數的底數)
恒成立時,求實數m的取值范圍(e為自然對數的底數)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將參加數學競賽決賽的500名同學編號為:001,002,…,500,采用系統抽樣的方法抽取一個容量為50的樣本,且隨機抽的號碼為003,這500名學生分別在三個考點考試,從001到200在第一考點,從201到355在第二考點,從356到500在第三考點,則第二考點被抽中的人數為( )
A.14
B.15
C.16
D.17
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以平面直角坐標系![]() 的原點為極點,
的原點為極點,![]() 軸的正半軸為極軸,建立極坐標系,兩種坐標系中取相同的長度單位.若直線
軸的正半軸為極軸,建立極坐標系,兩種坐標系中取相同的長度單位.若直線![]() 的參數方程為
的參數方程為![]() 為參數),曲線
為參數),曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(I)求直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(II)設直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點,若
兩點,若![]() 點的直角坐標為
點的直角坐標為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com