【題目】在直角坐標系
中，傾斜角為
的直線
經過坐標原點
，曲線
的參數方程為
（
為參數）.以點為極點，
軸的非負半軸為極軸建立極坐標系，曲線
的極坐標方程為
.
（1）求與的極坐標方程；
（2）設與的交點為、
，與的交點為、
，且
，求值.
科目：高中數學 來源： 題型：
【題目】某林場現有木材存量為
，每年以25%的增長率逐年遞增，但每年年底要砍伐的木材量為
，經過
年后林場木材存有量為
（1）求
的解析式
（2）為保護生態環境，防止水土流失，該地區每年的森林木材存量不應少于
，如果
，那么該地區會發生水土流失嗎？若會，要經過幾年？（取
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，正方體
，則下列四個命題:
①點
在直線
上運動，三棱錐
的體積不變
②點在直線上運動，直線
與平面
所成角的大小不變
③點在直線上運動，二面角
的大小不變
④點是平面
上到點
和
距離相等的動點，則的軌跡是過點
的直線.
其中的真命題是（ ）
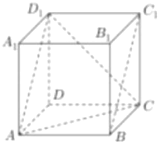
A.①③B.①③④C.①②④D.③④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了進一步推動全市學習型黨組織、學習型社會建設，某市組織開展“學習強國”知識測試，每人測試文化、經濟兩個項目，每個項目滿分均為60分.從全體測試人員中隨機抽取了100人，分別統計他們文化、經濟兩個項目的測試成績，得到文化項目測試成績的頻數分布表和經濟項目測試成績的頻率分布直方圖如下：
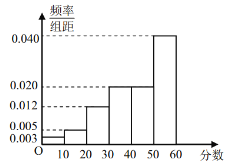
經濟項目測試成績頻率分布直方圖
分數區間 | 頻數 |
| 2 |
| 3 |
| 5 |
| 15 |
| 40 |
| 35 |
文化項目測試成績頻數分布表
將測試人員的成績劃分為三個等級如下：分數在區間
內為一般，分數在區間
內為良好，分數在區間
內為優秀.
（1）在抽取的100人中，經濟項目等級為優秀的測試人員中女生有14人，經濟項目等級為一般或良好的測試人員中女生有34人.填寫下面列聯表，并根據列聯表判斷是否有
以上的把握認為“經濟項目等級為優秀”與性別有關？
優秀 | 一般或良好 | 合計 | |
男生數 | |||
女生數 | |||
合計 |
（2）用這100人的樣本估計總體，假設這兩個項目的測試成績相互獨立.
（i）從該市測試人員中隨機抽取1人，估計其“文化項目等級高于經濟項目等級”的概率.
（ii）對該市文化項目、經濟項目的學習成績進行評價.
附：
| 0.150 | 0.050 | 0.010 |
| 2.072 | 3.841 | 6.635 |
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示的“8”字形曲線是由兩個關于
軸對稱的半圓和一個雙曲線的一部分組成的圖形，其中上半個圓所在圓方程是
，雙曲線的左、右頂點
、
是該圓與軸的交點，雙曲線與半圓相交于與軸平行的直徑的兩端點．
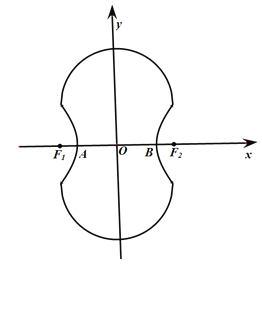
（1）試求雙曲線的標準方程；
（2）記雙曲線的左、右焦點為
、，試在“8”字形曲線上求點
，使得
是直角．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
為橢圓
上一點，
為橢圓長軸上一點，
為坐標原點，有下列結論：①存在點，，使得
為等邊三角形；②不存在點，，使得為等邊三角形；③存在點，，使得
；④不存在點，，使得.其中，所有正確結論的序號是( )
A.①④B.①③C.②④D.②③
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公交公司為了方便市民出行，科學規劃車輛投放，在一個人員密集流動地段增設一個起點站，為了研究車輛發車間隔時間x與乘客等候人數y之間的關系，經過調查得到如下數據：
間隔時間x/分 | 10 | 11 | 12 | 13 | 14 | 15 |
等候人數y/人 | 23 | 25 | 26 | 29 | 28 | 31 |
調查小組先從這6組數據中選取4組數據求線性回歸方程，再用剩下的2組數據進行檢驗.檢驗方法如下：先用求得的線性回歸方程計算間隔時間對應的等候人數
，再求與實際等候人數y的差，若差值的絕對值都不超過1，則稱所求方程是“恰當回歸方程”.
（1）從這6組數據中隨機選取4組數據，求剩下的2組數據的間隔時間相鄰的概率；
（2）若選取的是中間4組數據，求y關于x的線性回歸方程
，并判斷此方程是否是“恰當回歸方程”.
附：對于一組數據
，其回歸直線的斜率和截距的最小二乘估計分別為：
，
.
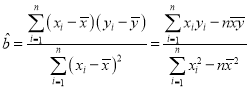查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校工會開展健步走活動，要求教職工上傳3月1日至3月7日微信記步數信息，下圖是職工甲和職工乙微信記步數情況：
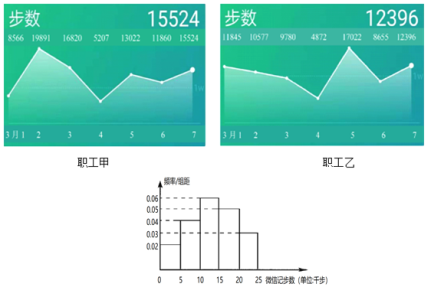
（Ⅰ）從3月1日至3月7日中任選一天，求這一天職工甲和職工乙微信記步數都不低于10000的概率；
（Ⅱ）從3月1日至3月7日中任選兩天，記職工乙在這兩天中微信記步數不低于10000的天數為
，求 的分布列及數學期望；
（Ⅲ）如圖是校工會根據3月1日至3月7日某一天的數據，制作的全校200名教職工微信記步數的頻率分布直方圖．已知這一天甲和乙微信記步數在單位200名教職工中排名分別為第68和第142，請指出這是根據哪一天的數據制作的頻率分布直方圖（不用說明理由）．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
