
【題目】某林場現有木材存量為![]() ,每年以25%的增長率逐年遞增,但每年年底要砍伐的木材量為
,每年以25%的增長率逐年遞增,但每年年底要砍伐的木材量為![]() ,經過
,經過![]() 年后林場木材存有量為
年后林場木材存有量為![]()
(1)求![]() 的解析式
的解析式
(2)為保護生態環境,防止水土流失,該地區每年的森林木材存量不應少于![]() ,如果
,如果![]() ,那么該地區會發生水土流失嗎?若會,要經過幾年?(取
,那么該地區會發生水土流失嗎?若會,要經過幾年?(取![]() )
)
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】高血壓高血糖和高血脂統稱“三高”.如圖是西南某地區從2010年至2016年患“三高”人數y(單位:千人)的折線圖.
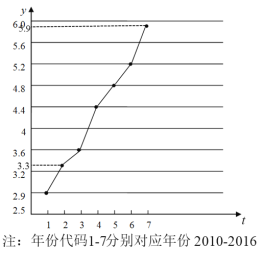
(1)由折線圖看出,可用線性回歸模型擬合![]() 與
與![]() 的關系,請求出相關系數(精確到0.01)并加以說明;
的關系,請求出相關系數(精確到0.01)并加以說明;
(2)建立![]() 關于
關于![]() 的回歸方程,預測2018年該地區患“三高”的人數.
的回歸方程,預測2018年該地區患“三高”的人數.
參考數據:![]() ,
,![]() ,
,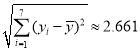 ,
,![]() .參考公式:相關系數
.參考公式:相關系數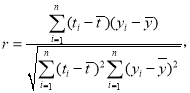 回歸方程
回歸方程![]() 中斜率和截距的最小二乘法估計公式分別為:
中斜率和截距的最小二乘法估計公式分別為:
![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司生產一種產品,每年投入固定成本0.5萬元,此外每生產100件這種產品還需要增加投資0.25萬元,經預測可知,市場對這種產品的年需求量為500件,當出售的這種產品的數量為t(單位:百件)時,銷售所得的收入約為![]() (萬元).
(萬元).
(1)若該公司的年產量為x(單位:百件),試把該公司生產并銷售這種產品所得的年利潤表示為年產量x的函數;
(2)當這種產品的年產量為多少時,當年所得利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》是我國古代數學文化的優秀遺產,數學家劉徽在注解《九章算術》時,發現當圓內接正多邊行的邊數無限增加時,多邊形的面積可無限逼近圓的面積,為此他創立了割圓術,利用割圓術,劉徽得到了圓周率精確到小數點后四位3.1416,后人稱3.14為徽率,如圖是利用劉徽的割圓術設計的程序框圖,若結束程序時,則輸出的![]() 為( )(
為( )(![]() ,
,![]() ,
,![]() )
)

A. 6 B. 12 C. 24 D. 48
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l:![]() 與拋物線C:
與拋物線C:![]() 相切.
相切.
(1)求拋物線方程;
(2)斜率不為0的直線![]() 經過拋物線C的焦點F,交拋物線于兩點A,B,拋物線C上是否存在兩點D,E關于直線
經過拋物線C的焦點F,交拋物線于兩點A,B,拋物線C上是否存在兩點D,E關于直線![]() 對稱.若存在求出斜率k的取值范圍;若不存在,說明理由.
對稱.若存在求出斜率k的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知奇函數f(x)![]() ,函數g(θ)=cos2θ+2sinθ
,函數g(θ)=cos2θ+2sinθ![]() ,θ∈[m,
,θ∈[m,![]() ].m,b∈R.
].m,b∈R.
(1)求b的值;
(2)判斷函數f(x)在[0,1]上的單調性,并證明;
(3)當x∈[0,1]時,函數g(θ)的最小值恰為f(x)的最大值,求m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com