【題目】圓周率是圓的周長與直徑的比值，一般用希臘字母
表示.早在公元480年左右，南北朝時期的數學家祖沖之就得出精確到小數點后7位的結果，他是世界上第一個把圓周率的數值計算到小數點后第7位的人，這比歐洲早了約1000年.生活中，我們也可以通過如下隨機模擬試驗來估計的值：在區(qū)間
內隨機取
個數，構成
個數對
，設
，
能與1構成鈍角三角形三邊的數對有
對，則通過隨機模擬的方法得到的的近似值為（ ）
A.
B.
C.
D.
核心素養(yǎng)學練評系列答案
單元期中期末卷系列答案科目：高中數學 來源： 題型：
【題目】已知函數f（x）＝（1﹣sinx）ex.
（1）求f（x）在區(qū)間（0，π）的極值；
（2）證明：函數g（x）＝f（x）﹣sinx﹣1在區(qū)間（﹣π，π）有且只有3個零點，且之和為0.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，直線
的參數方程為
（
為參數），以坐標原點為極點，
軸正半軸為極軸建立極坐標系，曲線
的極坐標方程是
.
（1）求曲線的直角坐標方程；
（2）已知點
，若直線與曲線交于不同的兩點
，當
最大時，求出直線的直角坐標方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
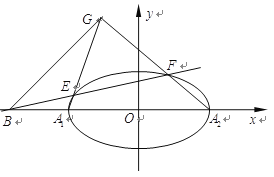
【題目】如圖，在平面直角坐標系
中，點
在橢圓
上，且橢圓的離心率為
.
（1）求橢圓
的標準方程；
（2）記橢圓的左、右頂點分別為
，過點
或
作一條直線交橢圓于
、
（不與重合）兩點，直線
交于點
，記直線
的斜率分別為
.
①對于給定的
，求
的值；
②是否存在一個定值
使得
恒成立，若存在，求出值；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】我國古代數學名著《算法統(tǒng)宗》中有如下問題：“遠望巍巍塔七層，紅光點點倍加增，共燈三百八十一，請問尖頭幾盞燈？”意思是：一座7層塔共掛了381盞燈，且相鄰兩層中的下一層燈數是上一層燈數的2倍，則塔的頂層共有燈（ ）
A. 1盞 B. 3盞 C. 5盞 D. 9盞
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】共享單車又稱為小黃車，近年來逐漸走進了人們的生活，也成為減少空氣污染，緩解城市交通壓力的一種重要手段．為調查某地區(qū)居民對共享單車的使用情況，從該地區(qū)居民中按年齡用隨機抽樣的方式隨機抽取了
人進行問卷調查，得到這人對共享單車的評價得分統(tǒng)計填入莖葉圖，如下所示（滿分
分）：
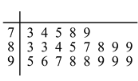
（1）找出居民問卷得分的眾數和中位數；
（2）請計算這位居民問卷的平均得分；
（3）若在成績?yōu)?/span>
分的居民中隨機抽取
人，求恰有
人成績超過
分的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中曲線
的參數方程為
（
為參數），以
為極點，
軸的正半軸為極軸，建立極坐標系，直線
的極坐標方程為
.
（1）求曲線的普通方程以及直線的直角坐標方程；
（2）將曲線向左平移2個單位，再將曲線上的所有點的橫坐標縮短為原來的
，得到曲線
，求曲線上的點到直線的距離的最小值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
