
【題目】已知關(guān)于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,則實(shí)數(shù)
上恒成立,則實(shí)數(shù)![]() 的取值范圍是_________.
的取值范圍是_________.
【答案】![]()
【解析】
分![]() 和
和![]() 兩種情況,結(jié)合函數(shù)
兩種情況,結(jié)合函數(shù)![]() 且
且![]() 在
在![]() 上恒正,將問(wèn)題轉(zhuǎn)化為不等式恒成立問(wèn)題,求出相應(yīng)的滿足條件的實(shí)數(shù)
上恒正,將問(wèn)題轉(zhuǎn)化為不等式恒成立問(wèn)題,求出相應(yīng)的滿足條件的實(shí)數(shù)![]() 的取值范圍,最后綜合討論的結(jié)果,可得實(shí)數(shù)
的取值范圍,最后綜合討論的結(jié)果,可得實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
若![]() ,
,
由函數(shù)![]() 在
在![]() 上恒正可得:
上恒正可得:![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,且
上恒成立,且![]() 在
在![]() 上恒成立,
上恒成立,
要使![]() 在
在![]() 上恒成立,則
上恒成立,則![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() ,
,
令![]() ,則
,則![]() ,
,![]() 在
在![]() 是單調(diào)遞增,所以當(dāng)
是單調(diào)遞增,所以當(dāng)![]() 時(shí),
時(shí),![]() 取得最大值
取得最大值![]() ,所以
,所以![]() ;
;
要使![]() 在
在![]() 上恒成立,則
上恒成立,則![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() ,
,
令![]() ,則
,則![]() ,
,![]() 在
在![]() 是單調(diào)遞增,所以當(dāng)
是單調(diào)遞增,所以當(dāng)![]() 時(shí),
時(shí),![]() 取得最小值
取得最小值![]() ,所以
,所以![]() ;
;
所以![]() ,
,
若![]() ,
,
由函數(shù)![]() 在
在![]() 上恒正可得,
上恒正可得,![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() ,
,
令![]() ,則
,則![]() ,
,![]() 在
在![]() 是單調(diào)遞增,所以當(dāng)
是單調(diào)遞增,所以當(dāng)![]() 時(shí),
時(shí),![]() 取得最大值
取得最大值![]() ,所以
,所以![]() ;
;
所以![]()
綜上可得:實(shí)數(shù)a的取值范圍為:![]() ,
,
故填:![]()


 同步學(xué)典一課多練系列答案
同步學(xué)典一課多練系列答案 經(jīng)典密卷系列答案
經(jīng)典密卷系列答案 金牌課堂練系列答案
金牌課堂練系列答案 三新快車金牌周周練系列答案
三新快車金牌周周練系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知命題:“若![]() ,則關(guān)于x的不等式
,則關(guān)于x的不等式![]() 的解集為空集”,那么它的逆命題,否命題,逆否命題,以及原命題中,假命題的個(gè)數(shù)是( )
的解集為空集”,那么它的逆命題,否命題,逆否命題,以及原命題中,假命題的個(gè)數(shù)是( )
A.0B.2C.3D.4
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知拋物線C1:x2=4y 的焦點(diǎn)F也是橢圓c2:![]() 的一個(gè)焦點(diǎn), C1和C2的公共弦長(zhǎng)為
的一個(gè)焦點(diǎn), C1和C2的公共弦長(zhǎng)為![]()
(1)求 C2的方程;
(2)過(guò)點(diǎn)F 的直線 l與 C1相交于A與B兩點(diǎn), 與C2相交于C , D兩點(diǎn),且![]() 與
與![]() 同向
同向
(ⅰ)若 ![]() 求直線l的斜率;
求直線l的斜率;
(ⅱ)設(shè) C1在點(diǎn) A處的切線與 x軸的交點(diǎn)為M ,證明:直線l 繞點(diǎn) F旋轉(zhuǎn)時(shí), ![]() MFD總是鈍角三角形。
MFD總是鈍角三角形。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】(2015·四川)某市A,B兩所中學(xué)的學(xué)生組隊(duì)參加辯論賽,A中學(xué)推薦3名男生,2名女生,B中學(xué)推薦了3名男生,4名女生,兩校推薦的學(xué)生一起參加集訓(xùn),由于集訓(xùn)后隊(duì)員的水平相當(dāng),從參加集訓(xùn)的男生中隨機(jī)抽取3人,女生中隨機(jī)抽取3人組成代表隊(duì)。
(1)求A中學(xué)至少有1名學(xué)生入選代表隊(duì)的概率.
(2)某場(chǎng)比賽前,從代表隊(duì)的6名隊(duì)員中隨機(jī)抽取4人參賽,設(shè)X表示參賽的男生人數(shù),求X得分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】(2015·陜西)如圖1,在直角梯形ABCD中,AD∥BC,![]() BAD=
BAD=![]() ,AB=BC=1,
,AB=BC=1,
AD=2, E是AD的中點(diǎn),0是AC與BE的交點(diǎn).將△ABE沿BE折起到△A1BE的位置,如圖2.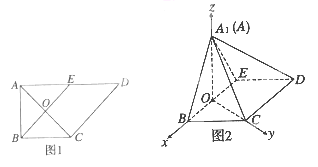
(1)證明:CD⊥平面A1OC
(2)若平面A1BE⊥平面BCDE, 四棱錐A1-BCDE的體積為36![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】(2015·陜西)如圖,橢圓E:![]() (a>b>0)經(jīng)過(guò)點(diǎn)A(0,-1),且離心率為
(a>b>0)經(jīng)過(guò)點(diǎn)A(0,-1),且離心率為![]() .
.
(1)求橢圓E的方程;
(2)經(jīng)過(guò)點(diǎn)(1,1),且斜率為k的直線與橢圓E交于不同兩點(diǎn)P,Q(均異于點(diǎn)A),證明:直線AP與AQ的斜率之和為2.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】(2015·江蘇)如圖,在平面直角坐標(biāo)系xOy中,已知橢圓![]() (a>b>0)的離心率為
(a>b>0)的離心率為![]() ,且右焦點(diǎn)F到左準(zhǔn)線l的距離為3.
,且右焦點(diǎn)F到左準(zhǔn)線l的距離為3.
(1)求橢圓的標(biāo)準(zhǔn)方程;
(2)過(guò)F的直線與橢圓交于A , B兩點(diǎn),線段AB的垂直平分線分別交直線l和AB于 點(diǎn)P , C , 若PC=2AB , 求直線AB的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為比較甲、乙兩地某月14時(shí)的氣溫狀況,隨機(jī)選取該月中的5天,將這5天中14時(shí)的氣溫?cái)?shù)據(jù)(單位:℃)制成如圖所示的莖葉圖.考慮以下結(jié)論:
據(jù)莖葉圖能得到的統(tǒng)計(jì)結(jié)論的標(biāo)號(hào)為( )
A.①③
B.①④
C.②③
D.②④
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)![]() ,求解下列問(wèn)題:(1)求
,求解下列問(wèn)題:(1)求![]() 的單調(diào)區(qū)間;(2)在銳角 △ A B C 中,角 ∠ A , B , C ,的對(duì)邊分別為 a , b , c ,若
的單調(diào)區(qū)間;(2)在銳角 △ A B C 中,角 ∠ A , B , C ,的對(duì)邊分別為 a , b , c ,若 ![]() = 0 , a = 1 ,求 △ A B C 面積的最大值.
= 0 , a = 1 ,求 △ A B C 面積的最大值.
(1)求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)在銳角![]() 中,角
中,角![]() ,的對(duì)邊分別為
,的對(duì)邊分別為![]() ,若
,若![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com