【題目】如圖，某生態(tài)園將一三角形地塊
的一角
開辟為水果園種植桃樹，已知角
為
,
的長度均大于
米，現(xiàn)在邊界
處建圍墻，在
處圍竹籬笆．
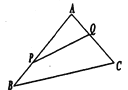
（1）若圍墻
總 長度為米，如何圍可使得三角形地塊
的面積最大？
（2）已知
段圍墻高
米，
段圍墻高
米，造價均為每平方米
元．若圍圍墻用了
元,問如何圍可使竹籬笆用料最省？
【答案】（1）當(dāng)
米,
米時, 可使三角形地塊
的面積最大；（2）當(dāng)
米,
米時, 可使籬笆最省．
【解析】
試題分析：（1）易得
的面積
．當(dāng)且僅當(dāng)
時，取“
”．即當(dāng)米；（2）由題意得
，要使竹籬笆用料最省，只需其長度
最短，又 
，當(dāng)
時,
有最小值
,從而求得正解．
試題解析：設(shè)
米，
米．
（1）則的面積
．
當(dāng)且僅當(dāng)
,即時，取“”．即當(dāng)米,米時, 可使三角形地塊的面積最大．
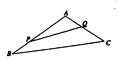
（2）由題意得
，即，要使竹籬笆用料最省，只需其長度最短，所以
，當(dāng)時, 有最小值,此時
當(dāng)米,米時, 可使籬笆最省．
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在一次籃球定點投籃訓(xùn)練中，規(guī)定每人最多投3次，在
處每投進(jìn)一球得3分；在
處每投進(jìn)一球得2分，如果前兩次得分之和超過3分就停止投籃；否則投第3次，某同學(xué)在
處的抽中率
，在
處的抽中率為
，該同學(xué)選擇現(xiàn)在
處投第一球，以后都在
處投，且每次投籃都互不影響，用
表示該同學(xué)投籃訓(xùn)練結(jié)束后所得的總分，其分布列為：
| 0 | 2 | 3 | 4 | 5 |
| 0.03 |
|
|
|
|
（1）求
的值；
（2）求隨機(jī)變量
的數(shù)學(xué)期望
；
（3）試比較該同學(xué)選擇上述方式投籃得分超過3分與選擇都在
處投籃得分超過3分的概率的大小．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，在四棱錐
中，
平面
，四邊形
為正方形，點
分別為線段
上的點，
．
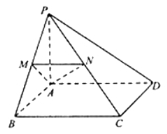
（1）求證：平面
平面
；
（2）求證：當(dāng)點
不與點
重合時，
平面
；
（3）當(dāng)
，
時，求點
到直線
距離的最小值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知
為坐標(biāo)原點，橢圓
：
的左、右焦點分別為
，右頂點為
,上頂點為
, 若
成等比數(shù)列，橢圓上的點到焦點
的最短距離為
．
（1）求橢圓的標(biāo)準(zhǔn)方程；
（2）設(shè)
為直線
上任意一點，過
的直線交橢圓于點
，且
，求
的最小值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】一青蛙從點
開始依次水平向右和豎直向上跳動，其落點坐標(biāo)依次是
，（如圖所示，坐標(biāo)以已知條件為準(zhǔn)），
表示青蛙從點
到點
所經(jīng)過的路程．
（1）若點為拋物線
（
）準(zhǔn)線上一點，點
均在該拋物線上，并且直線經(jīng)過該拋物線的焦點，證明
．
（2）若點
要么落在
所表示的曲線上，要么落在
所表示的曲線上，并且
,試寫出
（不需證明）；
（3）若點要么落在
所表示的曲線上，要么落在
所表示的曲線上，并且
，求
的表達(dá)式．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
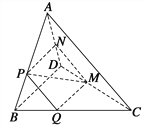
【題目】如圖，在四面體ABCD中，截面PQMN是正方形，則下列命題中，正確的為________ (填序號)．
①AC⊥BD；②AC∥截面PQMN；③AC＝BD；④異面直線PM與BD所成的角為45°.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓
的離心率為
，點
在橢圓
上．
（I）求橢圓
的方程；
（II）設(shè)動直線
與橢圓
有且僅有一個公共點，判斷是否存在以原點
為圓心的圓，滿足此圓與
相交于兩點
（兩點均不在坐標(biāo)軸上），且使得直線
的斜率之積為定值？若存在，求此圓的方程；若不存在，說明理由．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】
公司從某大學(xué)招收畢業(yè)生，經(jīng)過綜合測試，錄用了
名男生和
名女生，這
名畢業(yè)生的測試成績?nèi)缜o葉圖所示（單位：分），公司規(guī)定：成績在
分以上者到甲部門工作；
分以下者到乙部門工作，另外只有成績高于分才能擔(dān)任助理工作。
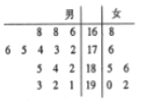
（1）如果用分層抽樣的方法從甲部門人選和乙部門人選中選取
人，再從這
人中選
人，那么至少有一人是甲部門人選的概率是多少？
（2）若從所有甲部門人選中隨機(jī)選
人，用
表示所選人員中能擔(dān)任助理工作的男生人數(shù)，寫出
的分布列，并求出的數(shù)學(xué)期望.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
