
【題目】如圖在正方體中![]() 中,
中,
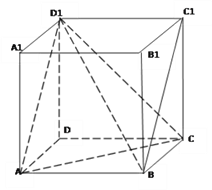
(1)求異面直線![]() 所成的角;
所成的角;
(2)求直線D1B與底面![]() 所成角的正弦值;
所成角的正弦值;
(3)求二面角![]() 大小的正切值.
大小的正切值.
【答案】(1) ![]() ; (2)
; (2)![]() ; (3)
; (3)![]() .
.
【解析】試題分析:(1)連接AC,AD1,∠AD1C即為BC1與CD1所成角;
(2)DD1⊥平面ABCD,∠D1DB為直線D1B與平面ABCD所成的角;
(3)連接BD交AC于O,則DO⊥AC,∠D1OD為二面角D1﹣AC﹣D的平面角.
試題解析:
(1)連接AC,AD1,如圖所示:

∵BC1∥AD1,
∴∠AD1C即為BC1與CD1所成角,
∵△AD1C為等邊三角形,
∴∠AD1C=60°,
故異面直線BC1與CD1所成的角為60°;
(2)∵DD1⊥平面ABCD,
∴∠D1DB為直線D1B與平面ABCD所成的角,
在Rt△D1DB中,sin∠D1DB=![]() =
=![]()
∴直線D1B與平面ABCD所成角的正弦值為![]() ;
;
(3)連接BD交AC于O,則DO⊥AC,
根據正方體的性質,D1D⊥面AC,
∴D1D⊥AC,D1D∩DO=D,
∴AC⊥面D1OD,∴AC⊥D1O,
∴∠D1OD為二面角D1﹣AC﹣D的平面角.
設正方體棱長為1,
在直角三角形D1OD中,DO=![]() ,DD1=1,
,DD1=1,
∴tan∠D1OD=![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,某生態園將一三角形地塊![]() 的一角
的一角![]() 開辟為水果園種植桃樹,已知角
開辟為水果園種植桃樹,已知角![]() 為
為![]() ,
,![]() 的長度均大于
的長度均大于![]() 米,現在邊界
米,現在邊界![]() 處建圍墻,在
處建圍墻,在![]() 處圍竹籬笆.
處圍竹籬笆.
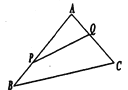
(1)若圍墻![]() 總 長度為
總 長度為![]() 米,如何圍可使得三角形地塊
米,如何圍可使得三角形地塊![]() 的面積最大?
的面積最大?
(2)已知![]() 段圍墻高
段圍墻高![]() 米,
米,![]() 段圍墻高
段圍墻高![]() 米,造價均為每平方米
米,造價均為每平方米![]() 元.若圍圍墻用了
元.若圍圍墻用了![]() 元,問如何圍可使竹籬笆用料最省?
元,問如何圍可使竹籬笆用料最省?
查看答案和解析>>
科目:高中數學 來源: 題型:
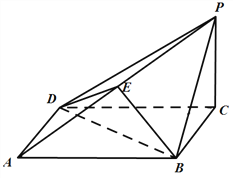
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為正方形,點
為正方形,點![]() 是棱
是棱![]() 的中點,
的中點,![]() ,平面
,平面![]()
![]() 平面
平面![]() .
.
(Ⅰ)求證:![]() //平面
//平面![]() ;
;
(Ⅱ)求證:![]() 平面
平面![]() ;
;
(Ⅲ) 設![]() ,試判斷平面
,試判斷平面![]() ⊥平面
⊥平面![]() 能否成立;若成立,寫出
能否成立;若成立,寫出![]() 的一個值(只需寫出結論).
的一個值(只需寫出結論).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中正確的是
A. 若直線![]() 與平面
與平面![]() 平行,則
平行,則![]() 與平面
與平面![]() 內的任意一條直線都沒有公共點;
內的任意一條直線都沒有公共點;
B. 若直線![]() 與平面
與平面![]() 平行,則
平行,則![]() 與平面
與平面![]() 內的任意一條直線都平行;
內的任意一條直線都平行;
C. 若直線![]() 上有無數個點不在平面
上有無數個點不在平面 ![]() 內,則
內,則![]() ;
;
D. 如果兩條平行線中的一條與一個平面平行,那么另一條也與這個平面平行.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設△ABC的三內角A,B,C的對邊分別是a,b,c,且b(sinB-sinC)+(c-a)(sinA+sinC)=0.
(Ⅰ)求角A的大小;
(Ⅱ)若![]() ,
,![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com