
圖1是一個正方體的表面展開圖,MN和PB是兩條面對角線,請在圖2的正方體中將MN和PB畫出來,并就這個正方體解決下列問題
(1) 求證:MN//平面PBD; (2)求證:AQ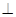 平面PBD;
平面PBD;
(3)求二面角P-DB-M的余弦值。
(1)只需證MN//BD;(2)只需證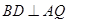 ,
, 。(3)
。(3) 。
。
解析試題分析:畫出MN和PB如圖所示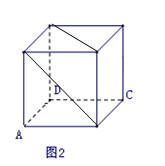
(1) 證明:在正方體ABCD-PMQN中 MN//BD
MN//BD
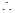 MN//平面PBD
MN//平面PBD
(2)證明:在正方體ABCD-PMQN中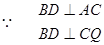

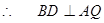
同理可證 : 

(3)解: 建立空間直角坐標(biāo)系如圖所示,設(shè)正方體的棱長為1
則 A(1,0,0), Q(0,1,1) , C(0,1,0)
由知平面PBD的一個法向量是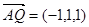
平面MBD的一個法向量是

 二面角P-DB-M的余弦值為
二面角P-DB-M的余弦值為  .
.
考點:正方體的的平面展開圖;線面平行的判定定理;線面垂直的判定定理;二面角。
點評:綜合法求二面角,往往需要作出平面角,這是幾何中一大難點,而用向量法求解二面角無需作出二面角的平面角,只需求出平面的法向量,經(jīng)過簡單運算即可,從而體現(xiàn)了空間向量的巨大作用.二面角的向量求法: ①若AB、CD分別是二面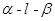 的兩個半平面內(nèi)與棱
的兩個半平面內(nèi)與棱 垂直的異面直線,則二面角的大小就是向量
垂直的異面直線,則二面角的大小就是向量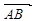 與
與 的夾角; ②設(shè)
的夾角; ②設(shè)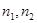 分別是二面角
分別是二面角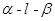 的兩個面α,β的法向量,則向量
的兩個面α,β的法向量,則向量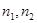 的夾角(或其補(bǔ)角)的大小就是二面角的平面角的大小。
的夾角(或其補(bǔ)角)的大小就是二面角的平面角的大小。


 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,圓錐 中,
中, 為底面圓的兩條直徑 ,AB交CD于O,且
為底面圓的兩條直徑 ,AB交CD于O,且 ,
, ,
, 為
為 的中點.
的中點.
(1)求證: 平面
平面 ;
;
(2)求圓錐 的表面積;求圓錐
的表面積;求圓錐 的體積。
的體積。
(3)求異面直線 與
與 所成角的正切值 .
所成角的正切值 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分) 已知一個四棱錐的三視圖如圖所示,其中 ,且
,且 ,
, 分別為
分別為 、
、 、
、 的中點
的中點
(1)求證:PB//平面EFG
(2)求直線PA與平面EFG所成角的大小
(3)在直線CD上是否存在一點Q,使二面角 的大小為
的大小為 ?若存在,求出CQ的長;若不存在,請說明理由。
?若存在,求出CQ的長;若不存在,請說明理由。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分14分)如圖,四棱錐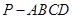 中,
中,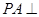 平面
平面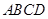 ,四邊形
,四邊形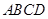 是矩形,
是矩形,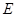 ,
,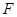 分別是
分別是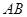 ,
,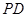 的中點.若
的中點.若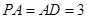 ,
,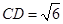 。
。
(1)求證: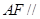 平面
平面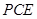 ;
;
(2)求直線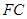 平面
平面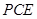 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
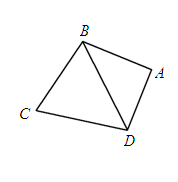
(本小題滿分12分)如圖4平面四邊形ABCD中,AB=AD=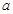 ,BC=CD=BD,設(shè)
,BC=CD=BD,設(shè)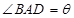 .
.
(1)將四邊形ABCD的面積S表示為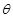 的函數(shù);
的函數(shù);
(2)求四邊形ABCD面積S的最大值及此時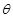 值.
值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題滿分10分) 如圖,在平行四邊形 中,
中, ,將
,將 沿
沿 折起到
折起到 的位置,使平面
的位置,使平面 平面
平面 .
.
(1)求二面角E-AB-D的大小;
(2)求四面體 的表面積和體積.
的表面積和體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分14分)如圖,在長方體 中,
中, ,
, ,點
,點 在棱
在棱 上移動.
上移動.
⑴ 證明: //平面
//平面 ;
;
⑵證明: ⊥
⊥ ;
;
⑶ 當(dāng) 為
為 的中點時,求四棱錐
的中點時,求四棱錐 的體積.
的體積.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com