
【題目】如圖,已知拋物線![]() 經(jīng)過點
經(jīng)過點![]() ,過點
,過點![]() 的直線
的直線![]() 與拋物線
與拋物線![]() 有兩個不同的交點
有兩個不同的交點![]() 、
、![]() .
.
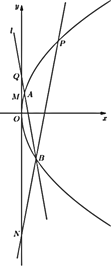
(1)求直線![]() 的斜率的取值范圍;
的斜率的取值范圍;
(2)設(shè)![]() 為原點,直線
為原點,直線![]() 交
交![]() 軸于
軸于![]() ,直線
,直線![]() 交
交![]() 軸于
軸于![]() ,
,![]() ,
,![]() ,求證:
,求證:![]() 為定值.
為定值.
【答案】(1)![]() ;(2)
;(2)![]() 為定值2,理由見解析.
為定值2,理由見解析.
【解析】
(1)將點P代入拋物線方程,即可求得p的值,設(shè)直線AB的方程,代入拋物線方程,由△>0,排除特殊情況,即可求得k的取值范圍;
(2)根據(jù)向量的共線定理即可求得λ=1﹣yM,μ=1﹣yN,求得直線PA的方程,令x=0,求得M點坐標(biāo),同理求得N點坐標(biāo),根據(jù)韋達定理和向量的坐標(biāo)表示,即可求得λ+μ為定值.
(1)拋物線C:y2=2px經(jīng)過點P(1,2),∴4=2p,解得p=2,
根據(jù)題意得過點(0,1)的直線斜率存在,設(shè)方程為y=kx+1,A(x1,y1),B(x2,y2);
聯(lián)立方程,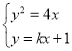 ,可得k2x2+(2k﹣4)x+1=0,
,可得k2x2+(2k﹣4)x+1=0,
∴△=(2k﹣4)2﹣4k2>0,且k≠0解得k<1,
故直線l的斜率的取值范圍(﹣∞,0)∪(0,1);
(2)設(shè)點M(0,yM),N(0,yN),則 ![]() (0,1﹣yM),
(0,1﹣yM),![]() (0,1);
(0,1);
因為![]() λ
λ![]() ,所以1=λ(1﹣yM),故λ
,所以1=λ(1﹣yM),故λ![]() ,同理μ
,同理μ![]() ,
,
直線PA的方程為y﹣2![]() (x﹣1)
(x﹣1)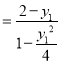 (x﹣1)
(x﹣1)![]() (x﹣1),
(x﹣1),
令x=0,得yM![]() ,同理可得yN
,同理可得yN![]() ,
,
因為λ+μ![]()
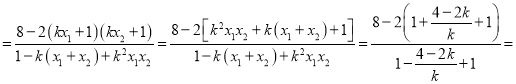 2,
2,
即有λ+μ為定值2.


 期末復(fù)習(xí)檢測系列答案
期末復(fù)習(xí)檢測系列答案 超能學(xué)典單元期中期末專題沖刺100分系列答案
超能學(xué)典單元期中期末專題沖刺100分系列答案 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案 陽光考場單元測試卷系列答案
陽光考場單元測試卷系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() 表示不大于實數(shù)
表示不大于實數(shù)![]() 的最大整數(shù),函數(shù)
的最大整數(shù),函數(shù)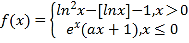 ,若關(guān)于
,若關(guān)于![]() 的方程
的方程![]() 有且只有5個解,則實數(shù)
有且只有5個解,則實數(shù)![]() 的取值范圍為( )
的取值范圍為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)A是同時符合以下性質(zhì)的函數(shù)f(x)組成的集合:
①x∈[0,+∞),都有f(x)∈(1,4];②f(x)在[0,+∞)上是減函數(shù).
(1)判斷函數(shù)f1(x)=2-![]() 和f2(x)=1+3·
和f2(x)=1+3·![]() (x≥0)是否屬于集合A,并簡要說明理由;
(x≥0)是否屬于集合A,并簡要說明理由;
(2)把(1)中你認(rèn)為是集合A中的一個函數(shù)記為g(x),若不等式g(x)+g(x+2)≤k對任意的x≥0總成立,求實數(shù)k的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,其中
,其中![]() 為常數(shù).
為常數(shù).
(1)證明: ![]() ;
;
(2)是否存在![]() ,使得
,使得![]() 為等差數(shù)列?并說明理由.
為等差數(shù)列?并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列說法中:
①若![]() ,滿足
,滿足![]() ,則
,則![]() 的最大值為
的最大值為![]() ;
;
②若![]() ,則函數(shù)
,則函數(shù)![]() 的最小值為
的最小值為![]()
③若![]() ,滿足
,滿足![]() ,則
,則![]() 的最小值為
的最小值為![]()
④函數(shù)![]() 的最小值為
的最小值為![]()
正確的有__________.(把你認(rèn)為正確的序號全部寫上)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() 且
且![]() ).
).
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)若![]() ,討論函數(shù)
,討論函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最值.
上的最值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某班主任對全班50名學(xué)生進行了作業(yè)量多少的調(diào)查,喜歡玩電腦游戲的同學(xué)認(rèn)為作業(yè)多的有18人,認(rèn)為作業(yè)不多的有9人,不喜歡玩電腦游戲的同學(xué)認(rèn)為作業(yè)多的有8人,認(rèn)為作業(yè)不多的有15人,則認(rèn)為喜歡玩電腦游戲與認(rèn)為作業(yè)量的多少有關(guān)系的把握大約是多少?
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為考查某種疫苗預(yù)防疾病的效果,進行動物實驗,得到統(tǒng)計數(shù)據(jù)如下:
未發(fā)病 | 發(fā)病 | 總計 | |
未注射疫苗 | 20 |
|
|
注射疫苗 | 30 |
|
|
總計 | 50 | 50 | 100 |
現(xiàn)從所有試驗動物中任取一只,取到“注射疫苗”動物的概率為![]() .
.
(1)求![]() 列聯(lián)表中的數(shù)據(jù)
列聯(lián)表中的數(shù)據(jù)![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)判斷疫苗是否有效?
(3)能夠有多大把握認(rèn)為疫苗有效?
(參考公式![]() ,
,![]() )
)
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com