
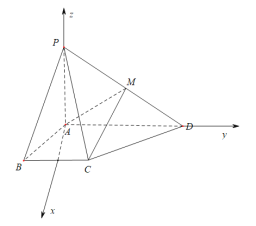
【題目】如圖,在四棱錐![]() 中,
中,![]() 底面
底面![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 是棱
是棱![]() 的中點(diǎn).
的中點(diǎn).
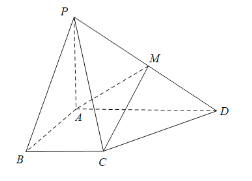
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小.
的大小.
【答案】(1)見解析(2)![]()
【解析】
(1)取![]() 的中點(diǎn)
的中點(diǎn)![]() ,連接
,連接![]() 、
、![]() ,證明四邊形
,證明四邊形![]() 為平行四邊形,即可證明
為平行四邊形,即可證明![]() 平面
平面![]() .
.
(2)以![]() 為坐標(biāo)原點(diǎn),
為坐標(biāo)原點(diǎn),![]() ,
,![]() ,
,![]() 所在的直線分別為
所在的直線分別為![]() 軸、
軸、![]() 軸、
軸、![]() 軸建立如圖所示的空間直角坐標(biāo)系,求出平面
軸建立如圖所示的空間直角坐標(biāo)系,求出平面![]() 的一個法向量
的一個法向量![]() ,取平面
,取平面![]() 的一個法向量為
的一個法向量為![]() ,結(jié)合空間向量數(shù)量積運(yùn)算即可得解.
,結(jié)合空間向量數(shù)量積運(yùn)算即可得解.
證明:(1)如圖,取![]() 的中點(diǎn)
的中點(diǎn)![]() ,連接
,連接![]() 、
、![]() .
.
∵![]() 是
是![]() 的中點(diǎn),∴
的中點(diǎn),∴![]() ,
,![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
∴四邊形![]() 為平行四邊形,
為平行四邊形,
∴![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
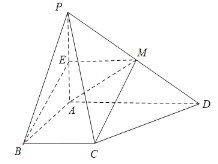
(2)在平面![]() 內(nèi)過點(diǎn)
內(nèi)過點(diǎn)![]() 作
作![]() 的垂線
的垂線![]() ,由題意知
,由題意知![]() ,
,![]() ,
,![]() 兩兩垂直,以
兩兩垂直,以
![]() 為坐標(biāo)原點(diǎn),
為坐標(biāo)原點(diǎn),![]() ,
,![]() ,
,![]() 所在的直線分別為
所在的直線分別為![]() 軸、
軸、![]() 軸、
軸、![]() 軸建立如圖所示的空
軸建立如圖所示的空
間直角坐標(biāo)系,由題意知![]() ,
,![]() ,
,![]() ,
,
可得![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
設(shè)平面![]() 的法向量為
的法向量為![]() ,
,
則由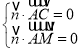 ,即
,即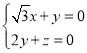 ,令
,令![]() ,則
,則![]() ,
,![]() ,
,
∴![]() 為平面
為平面![]() 的一個法向量.
的一個法向量.
∵![]() 底面
底面![]() ,∴可取平面
,∴可取平面![]() 的一個法向量為
的一個法向量為![]() ,
,
∴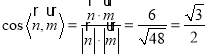 ,
,
∵二面角![]() 為銳二面角,
為銳二面角,
∴二面角![]() 的大小為
的大小為![]() .
.


 名校課堂系列答案
名校課堂系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】杭州西溪國家濕地公園是以水為主題的公園,以濕地良好生態(tài)環(huán)境和多樣化濕地景觀資源為基礎(chǔ)的生態(tài)型主題公園.欲在該公園內(nèi)搭建一個平面凸四邊形![]() 的休閑觀光及科普宣教的平臺,如圖所示,其中
的休閑觀光及科普宣教的平臺,如圖所示,其中![]() 百米,
百米,![]() 百米,
百米,![]() 為正三角形.建成后
為正三角形.建成后![]() 將作為人們旅游觀光休閑娛樂的區(qū)域,
將作為人們旅游觀光休閑娛樂的區(qū)域,![]() 將作為科普宣教濕地功能利用弘揚(yáng)濕地文化的區(qū)域.
將作為科普宣教濕地功能利用弘揚(yáng)濕地文化的區(qū)域.
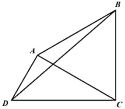
(1)當(dāng)![]() 時,求旅游觀光休閑娛樂的區(qū)域
時,求旅游觀光休閑娛樂的區(qū)域![]() 的面積;
的面積;
(2)求旅游觀光休閑娛樂的區(qū)域![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點(diǎn)分別為
的左、右焦點(diǎn)分別為![]() ,
,![]() .過焦點(diǎn)且垂直于
.過焦點(diǎn)且垂直于![]() 軸的直線與橢圓
軸的直線與橢圓![]() 相交所得的弦長為3,直線
相交所得的弦長為3,直線![]() 與橢圓
與橢圓![]() 相切.
相切.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)設(shè)過點(diǎn)![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() ,
,![]() 兩點(diǎn),若
兩點(diǎn),若![]() ,問直線
,問直線![]() 是否存在?若存在,求直線
是否存在?若存在,求直線![]() 的斜率
的斜率![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為頂點(diǎn)的五面體中,平面
為頂點(diǎn)的五面體中,平面![]() 平面
平面![]() ,
,![]() ,四邊形
,四邊形![]() 為平行四邊形,且
為平行四邊形,且![]() .
.

(1)求證:![]() ;
;
(2)若![]() ,
,![]() ,直線
,直線![]() 與平面
與平面![]() 所成角為60°,求平面
所成角為60°,求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某同學(xué)計(jì)劃用他姓名的首字母![]() ,身份證的后4位數(shù)字(4位數(shù)字都不同)以及3個符號
,身份證的后4位數(shù)字(4位數(shù)字都不同)以及3個符號![]() 設(shè)置一個六位的密碼.若
設(shè)置一個六位的密碼.若![]() 必選,且符號不能超過兩個,數(shù)字不能放在首位和末位,字母和數(shù)字的相對順序不變,則他可設(shè)置的密碼的種數(shù)為( )
必選,且符號不能超過兩個,數(shù)字不能放在首位和末位,字母和數(shù)字的相對順序不變,則他可設(shè)置的密碼的種數(shù)為( )
A.864B.1009C.1225D.1441
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知衡量病毒傳播能力的最重要指標(biāo)叫做傳播指數(shù)RO.它指的是,在自然情況下(沒有外力介入,同時所有人都沒有免疫力),一個感染到某種傳染病的人,會把疾病傳染給多少人的平均數(shù).它的簡單計(jì)算公式是:![]() 確認(rèn)病例增長率
確認(rèn)病例增長率![]() 系列間隔,其中系列間隔是指在一個傳播鏈中,兩例連續(xù)病例的間隔時間(單位:天).根據(jù)統(tǒng)計(jì),確認(rèn)病例的平均增長率為
系列間隔,其中系列間隔是指在一個傳播鏈中,兩例連續(xù)病例的間隔時間(單位:天).根據(jù)統(tǒng)計(jì),確認(rèn)病例的平均增長率為![]() ,兩例連續(xù)病例的間隔時間的平均數(shù)為
,兩例連續(xù)病例的間隔時間的平均數(shù)為![]() 天,根據(jù)以上RO數(shù)據(jù)計(jì)算,若甲得這種傳染病,則
天,根據(jù)以上RO數(shù)據(jù)計(jì)算,若甲得這種傳染病,則![]() 輪傳播后由甲引起的得病的總?cè)藬?shù)約為( )
輪傳播后由甲引起的得病的總?cè)藬?shù)約為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,已知曲線
中,已知曲線![]() 的參數(shù)方程:
的參數(shù)方程: (
(![]() 為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),以
為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),以![]() 軸的正半軸為極軸建立極坐標(biāo)系,曲線
軸的正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求曲線![]() 的普通方程;
的普通方程;
(2)過曲線![]() 上一點(diǎn)
上一點(diǎn)![]() 作直線
作直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點(diǎn),中點(diǎn)為
兩點(diǎn),中點(diǎn)為![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是等腰梯形,
是等腰梯形,![]() ,
,![]() ,
,![]() 是等邊三角形,點(diǎn)
是等邊三角形,點(diǎn)![]() 在
在![]() 上,且
上,且![]() .
.

(1)證明:![]() //平面
//平面![]() .
.
(2)若平面![]() 平面
平面![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com