
【題目】某地隨著經濟的發展,居民收入逐年增大,下表是該地一農業銀行連續五年的儲蓄存款(年底余額),如下表:

為了研究方便,工作人員將上表的數據進行了處理,![]() ,得到下表:
,得到下表:

(1)求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(3)用所求回歸方程預測,到2020年底,該地儲蓄存款額大約可達多少?
(附:線性回歸方程:![]() ,
,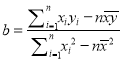 ,
,![]() )
)
【答案】(1)![]() (2)
(2)![]() (3)到2020年底,該地儲蓄存款額大約可達13.2億元.
(3)到2020年底,該地儲蓄存款額大約可達13.2億元.
【解析】
(1)由題意計算平均數與回歸系數,寫出y關于t的回歸方程;
(2)由t=x﹣2012,代入(1)中回歸方程求得y關于x的回歸方程;
(3)將x=2020代入回歸方程求得![]() 的值即可.
的值即可.
解:(1)由題意計算![]() 3,
3,![]() 7.2,
7.2,
![]() tiyi=120,
tiyi=120,![]() 55,
55,
∵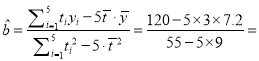 1.2,
1.2,
![]() 7.2﹣1.2×3=3.6,
7.2﹣1.2×3=3.6,
∴y關于t的線性回歸方程為![]() 1.2t+3.6;
1.2t+3.6;
(2)∵t=x﹣2012與![]() 1.2t+3.6,
1.2t+3.6,
∴![]() 1.2(x﹣2012)+3.6,
1.2(x﹣2012)+3.6,
即y關于x的線性回歸方程為![]() 1.2x﹣2410.8;
1.2x﹣2410.8;
(3)將x=2020代入![]() 1.2x﹣2410.8,
1.2x﹣2410.8,
計算得![]() 1.2×2020﹣2410.8=13.2,
1.2×2020﹣2410.8=13.2,
所以到2020年底,該地儲蓄存款額大約可達13.2億元.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知動點M(x,y)滿足![]() ,點M的軌跡為曲線E.
,點M的軌跡為曲線E.
(1)求E的標準方程;
(2)過點F(1,0)作直線交曲線E于P,Q兩點,交![]() 軸于R點,若
軸于R點,若![]() ,證明:
,證明:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的幾何體ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥ AB,M是EC上的點(不與端點重合),F為DA上的點,N為BE的中點.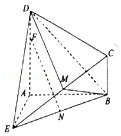
(Ⅰ)若M是EC的中點,AF=3FD,求證:FN∥平面MBD;
(Ⅱ)若平面MBD與平面ABD所成角(銳角)的余弦值為 ![]() ,試確定點M在EC上的位置.
,試確定點M在EC上的位置.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的前
的前![]() 項和為
項和為![]() ,滿足
,滿足![]() ,
,![]() .數列
.數列![]() 滿足
滿足![]() ,
,![]() ,且
,且![]() .
.
(1)求數列![]() 和
和![]() 的通項公式;
的通項公式;
(2)若![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() ,對任意的
,對任意的![]() ,都有
,都有![]() ,求實數
,求實數![]() 的取值范圍;
的取值范圍;
(3)是否存在正整數![]() ,
,![]() ,使
,使![]() ,
,![]() ,
,![]() (
(![]() )成等差數列,若存在,求出所有滿足條件的
)成等差數列,若存在,求出所有滿足條件的![]() ,
,![]() ,若不存在,請說明理由.
,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() ﹣m(lnx+
﹣m(lnx+ ![]() )(m為實數,e=2.71828…是自然對數的底數). (Ⅰ)當m>1時,討論f(x)的單調性;
)(m為實數,e=2.71828…是自然對數的底數). (Ⅰ)當m>1時,討論f(x)的單調性;
(Ⅱ)若g(x)=x2f′(x)﹣xex在( ![]() ,3)內有兩個零點,求實數m的取值范圍.
,3)內有兩個零點,求實數m的取值范圍.
(Ⅲ)當m=1時,證明:xf(x)+xlnx+1>x+ ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() ,
,![]() ,若
,若![]() 對任意
對任意![]() 成立,則下列命題中正確的命題個數是( )
成立,則下列命題中正確的命題個數是( )
(1)![]()
(2)![]()
(3)![]() 不具有奇偶性
不具有奇偶性
(4)![]() 的單調增區間是
的單調增區間是![]()
(5)可能存在經過點![]() 的直線與函數的圖象不相交
的直線與函數的圖象不相交
A. 1個B. 2個C. 3個D. 4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=Acos(ωx+φ)(A>0,ω>0,﹣π<φ<0)的部分圖象如圖所示,為了得到g(x)=Acosωx的圖象,只需將函數y=f(x)的圖象( ) 
A.向左平移 ![]() 個單位長度
個單位長度
B.向左平移 ![]() 個單位長度
個單位長度
C.向右平移 ![]() 個單位長度
個單位長度
D.向右平移 ![]() 個單位長度
個單位長度
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(Ⅰ)若曲線![]() 在
在![]() 處的切線與直線
處的切線與直線![]() 平行,求實數
平行,求實數![]() 的值;
的值;
(Ⅱ)若函數![]() 在定義域上為增函數,求實數
在定義域上為增函數,求實數![]() 的取值范圍;
的取值范圍;
(Ⅲ)若![]() 有兩個極值點
有兩個極值點![]() ,且
,且![]() ,
,![]() ,若不等式
,若不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com