
【題目】已知函數f(x)=sin(x﹣ ![]() )cos(x﹣
)cos(x﹣ ![]() )(x∈R),則下面結論錯誤的是( )
)(x∈R),則下面結論錯誤的是( )
A.函數f(x)的圖象關于點(﹣ ![]() ,0)對稱
,0)對稱
B.函數f(x)的圖象關于直線x=﹣ ![]() 對稱
對稱
C.函數f(x)在區間[0, ![]() ]上是增函數
]上是增函數
D.函數f(x)的圖象是由函數y= ![]() sin2x的圖象向右平移
sin2x的圖象向右平移 ![]() 個單位而得到
個單位而得到
【答案】A
【解析】解:∵函數f(x)=sin(x﹣ ![]() )cos(x﹣
)cos(x﹣ ![]() )=
)= ![]() sin(2x﹣
sin(2x﹣ ![]() ),令x=﹣
),令x=﹣ ![]() ,可得2x﹣
,可得2x﹣ ![]() =﹣
=﹣ ![]() ,f(x)≠0,
,f(x)≠0,
故函數f(x)的圖象不關于點(﹣ ![]() ,0)對稱,故A錯誤.
,0)對稱,故A錯誤.
令x=﹣ ![]() ,可得2x﹣
,可得2x﹣ ![]() =﹣
=﹣ ![]() ,f(x)=0,故函數f(x)的圖象關于點(﹣
,f(x)=0,故函數f(x)的圖象關于點(﹣ ![]() ,0)對稱,故B正確.
,0)對稱,故B正確.
令x∈[0, ![]() ],可得2x﹣
],可得2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],故函數f(x)在區間[0,
],故函數f(x)在區間[0, ![]() ]上是增函數,故C正確.
]上是增函數,故C正確.
把函數y= ![]() sin2x的圖象向右平移
sin2x的圖象向右平移 ![]() 個單位,可得y=
個單位,可得y= ![]() sin(2x﹣
sin(2x﹣ ![]() ) 的圖象,故D正確,
) 的圖象,故D正確,
故選:A.
【考點精析】關于本題考查的函數y=Asin(ωx+φ)的圖象變換,需要了解圖象上所有點向左(右)平移![]() 個單位長度,得到函數
個單位長度,得到函數![]() 的圖象;再將函數
的圖象;再將函數![]() 的圖象上所有點的橫坐標伸長(縮短)到原來的
的圖象上所有點的橫坐標伸長(縮短)到原來的![]() 倍(縱坐標不變),得到函數
倍(縱坐標不變),得到函數![]() 的圖象;再將函數
的圖象;再將函數![]() 的圖象上所有點的縱坐標伸長(縮短)到原來的
的圖象上所有點的縱坐標伸長(縮短)到原來的![]() 倍(橫坐標不變),得到函數
倍(橫坐標不變),得到函數![]() 的圖象才能得出正確答案.
的圖象才能得出正確答案.


 名師金手指領銜課時系列答案
名師金手指領銜課時系列答案科目:高中數學 來源: 題型:
【題目】某同學使用計算器求30個數據的平均數時,錯將其中一個數據105輸入為15,那么由此求出的平均數與實際平均數的差是( )
A.35
B.﹣3
C.3
D.﹣0.5
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】運貨卡車以每小時x千米的速度勻速行駛130千米(50≤x≤100)(單位:千米/小時).假設汽油的價格是每升2元,而汽車每小時耗油(2+ ![]() )升,司機的工資是每小時14元.
)升,司機的工資是每小時14元.
(1)求這次行車總費用y關于x的表達式;
(2)當x為何值時,這次行車的總費用最低,并求出最低費用的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【廣西名校2017屆高三上學期第一次摸底】如圖,過拋物線![]() 上一點
上一點![]() ,作兩條直線分別交拋物線于
,作兩條直線分別交拋物線于![]() ,
,![]() ,
,
當![]() 與
與![]() 的斜率存在且傾斜角互補時:
的斜率存在且傾斜角互補時:
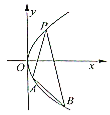
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若直線![]() 在
在![]() 軸上的截距
軸上的截距![]() 時,求
時,求![]() 面積
面積![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點P(x、y)滿足
(1)若x∈{0,1,2,3,4,5},y∈{0,1,2,3,4},則求y≥x的概率.
(2)若x∈[0,5],y∈[0,4],則求x>y的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為橢圓
為橢圓![]() 的左右焦點,點
的左右焦點,點![]() 為其上一點,且有
為其上一點,且有![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,過
兩點,過![]() 與
與![]() 平行的直線
平行的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,求四邊形
兩點,求四邊形![]() 的面積
的面積![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖甲所示, ![]() 是梯形
是梯形![]() 的高,
的高, ![]() ,
, ![]() ,
, ![]() ,現將梯形
,現將梯形![]() 沿
沿![]() 折起如圖乙所示的四棱錐
折起如圖乙所示的四棱錐![]() ,使得
,使得![]() ,點
,點![]() 是線段
是線段![]() 上一動點.
上一動點.
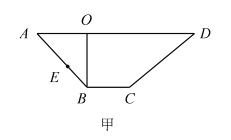
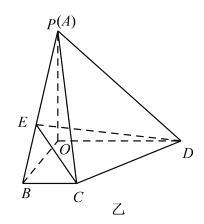
(1)證明: ![]() 和
和![]() 不可能垂直;
不可能垂直;
(2)當![]() 時,求
時,求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com