
【題目】將一枚棋子放在一個![]() 的棋盤上,記
的棋盤上,記![]() 為從左、上數第
為從左、上數第![]() 行第
行第![]() 列的小方格,求所有的四元數組
列的小方格,求所有的四元數組![]() ,使得從
,使得從![]() 出發,經過每個小方格恰一次到達
出發,經過每個小方格恰一次到達![]() (每步為將棋子從一個小方格移到與之有共同邊的另一個小方格).
(每步為將棋子從一個小方格移到與之有共同邊的另一個小方格).
【答案】所求為![]() ,且當
,且當![]() 為偶數時,
為偶數時,![]() ;當
;當![]() 為奇數時,
為奇數時,![]() .
.
【解析】
將![]() 棋盤按國際象棋方式黑邊相間染色,其中,
棋盤按國際象棋方式黑邊相間染色,其中,![]() 為黑色,
為黑色,
當![]() 為奇數時,任兩個黑色的小方格滿足條件,當
為奇數時,任兩個黑色的小方格滿足條件,當![]() 為偶數時,任兩個異色的小方格滿足條件.
為偶數時,任兩個異色的小方格滿足條件.
記以下結論為![]() .
.
下面用數學歸納法證明,
先證下面的引理.
引理1 ![]() 與
與![]() 等價
等價
顯然成立.
引理2 在![]() 棋盤中,不同列的異色的兩個小方格滿足條件.
棋盤中,不同列的異色的兩個小方格滿足條件.
引理2的證明:若![]() 同行,因二者異色,則其中間有偶數列,由如圖方式知
同行,因二者異色,則其中間有偶數列,由如圖方式知![]() 滿足條件.
滿足條件.
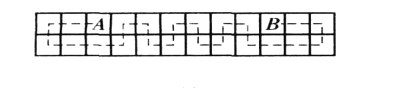
若![]() 不同行,因二者異色,則其中間有奇數列,由如圖方式知
不同行,因二者異色,則其中間有奇數列,由如圖方式知![]() 滿足條件.
滿足條件.
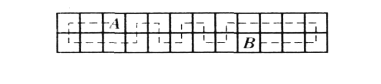
引理3 若![]() 成立,則
成立,則![]() 成立,
成立,
引理3的證明:對![]() 棋盤,分兩種情況討論:
棋盤,分兩種情況討論:
(1)若![]() 都不在前(后)兩列,則在后(前)面的
都不在前(后)兩列,則在后(前)面的![]() 棋盤中,有
棋盤中,有![]() 成立,且在前(后)第三列中必有相鄰方格是
成立,且在前(后)第三列中必有相鄰方格是![]() 中棋子走過的路徑中連續的兩個方格(設為
中棋子走過的路徑中連續的兩個方格(設為![]() ),可用如圖
),可用如圖
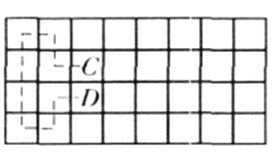
方式將前(后)兩列并入棋子原來的路徑,使![]() 成立.
成立.
(2)若![]() 一個在前兩列,另一個在后兩列,不妨設
一個在前兩列,另一個在后兩列,不妨設![]() 在前兩列,則在第二列有至少兩個方格與
在前兩列,則在第二列有至少兩個方格與![]() 異色,其中至少有一個方格(記為
異色,其中至少有一個方格(記為![]() )與
)與![]() 不同行,由引理
不同行,由引理![]() 知在前
知在前![]() 棋盤中,
棋盤中,![]() 滿足條件,取第三列中與
滿足條件,取第三列中與![]() 相鄰的方格
相鄰的方格![]() (與
(與![]() 同色),則由
同色),則由![]() 成立,知在后
成立,知在后![]() 棋盤中,
棋盤中,![]() 滿足條件.
滿足條件.
故由![]() ,使
,使![]() 成立.
成立.
由(1)、(2)知![]() 成立.
成立.
類似可證:
引理4 若![]() 成立,則
成立,則![]() 成立.
成立.
回到原題
由引理![]() 知,為利用數學歸納法,只需證明
知,為利用數學歸納法,只需證明![]() 成立即可.
成立即可.
對![]() 異色.
異色.
若![]() 相鄰,則由如圖
相鄰,則由如圖
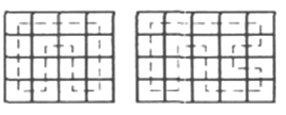
環路知![]() 滿足條件.
滿足條件.
若![]() 不相鄰,當
不相鄰,當![]() 都在上(下)兩行時,由引理2知在
都在上(下)兩行時,由引理2知在![]() 棋盤中,
棋盤中,![]() 滿足條件.
滿足條件.
類似引理3
(1)知有![]() 的路徑使
的路徑使![]() 成立,當
成立,當![]() 一個在上兩行,另一個在下兩行時,類似引理3(2)知有
一個在上兩行,另一個在下兩行時,類似引理3(2)知有
![]() 的路徑使
的路徑使![]() 成立.
成立.
對![]() ,
,![]() 同黑.
同黑.
先由圖知![]() 成立.
成立.
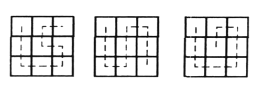
再分兩種情況證![]() 成立.
成立.
若![]() 都在前(后)三列,則由
都在前(后)三列,則由![]() 成立,知在前(后)
成立,知在前(后)![]() 棋盤中,
棋盤中,![]() 滿足條件,類似引理3(1)知在
滿足條件,類似引理3(1)知在![]() 棋盤中有
棋盤中有![]() 路徑使
路徑使![]() 成立.
成立.
若![]() 一個在前兩列,另一個在后兩列,不妨設
一個在前兩列,另一個在后兩列,不妨設![]() 在前兩列,由引理2知,在第2列中存在白方格
在前兩列,由引理2知,在第2列中存在白方格![]() ,在第4列中存在白方格
,在第4列中存在白方格![]() ,使得分別在前、后
,使得分別在前、后![]() 棋盤中,
棋盤中,![]() 、
、![]() 分別滿足條件,如圖
分別滿足條件,如圖
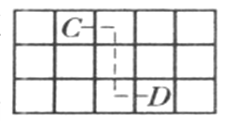
方式將![]() 、
、![]() 相連,則
相連,則![]() 使
使![]() 成立.
成立.
最后分兩種情況證![]() 成立.
成立.
若![]() 都在前(后)三列,則由
都在前(后)三列,則由![]() 成立,類似引理
成立,類似引理![]() 可知在
可知在![]() 棋盤中,有
棋盤中,有![]() 路徑使
路徑使![]() 成立.
成立.
若![]() 一個在前兩列,另一個在后兩列,類似
一個在前兩列,另一個在后兩列,類似![]() 中第2種情況知在
中第2種情況知在![]() 棋盤中有
棋盤中有![]() 路徑使
路徑使![]() 成立.
成立.
故![]() 成立.
成立.
綜上,所求為![]() ,且當
,且當![]() 為偶數時,
為偶數時,![]() ;
;
當![]() 為奇數時,
為奇數時,![]() .
.


科目:高中數學 來源: 題型:
【題目】已知數列![]() 的前
的前![]() 項和為
項和為![]() ,且滿足
,且滿足![]() .
.
(1)求數列![]() 的通項.
的通項.
(2)若![]() ,求數列
,求數列![]() 的最大值項.
的最大值項.
(3)對于(2)中數列![]() ,是否存在
,是否存在![]() ?若存在,求出所有相等的兩項;若不存在,說明理由.
?若存在,求出所有相等的兩項;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】四棱錐![]() 中,
中,![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,BC//AD,已知Q是四邊形ABCD內部一點,且二面角
,BC//AD,已知Q是四邊形ABCD內部一點,且二面角![]() 的平面角大小為
的平面角大小為![]() ,若動點Q的軌跡將ABCD分成面積為
,若動點Q的軌跡將ABCD分成面積為![]() 的兩部分,則
的兩部分,則![]() =_______.
=_______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】
已知雙曲線![]() 設過點
設過點![]() 的直線l的方向向量
的直線l的方向向量![]()
(1) 當直線l與雙曲線C的一條漸近線m平行時,求直線l的方程及l與m的距離;
(2) 證明:當![]() >
>![]() 時,在雙曲線C的右支上不存在點Q,使之到直線l的距離為
時,在雙曲線C的右支上不存在點Q,使之到直線l的距離為![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,求:
,求:
(1)過點![]() 與原點距離為2的直線
與原點距離為2的直線![]() 的方程;
的方程;
(2)過點![]() 與原點距離最大的直線
與原點距離最大的直線![]() 的方程,最大距離是多少?
的方程,最大距離是多少?
(3)是否存在過點![]() 與原點距離為6的直線?若存在,求出方程;若不存在,請說明理由.
與原點距離為6的直線?若存在,求出方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了考察冰川的融化狀況,一支科考隊在某冰川山上相距8km的A、B兩點各建一個考察基地,視冰川面為平面形,以過A、B兩點的直線為x軸,線段AB的垂直平分線為y軸建立平面直角坐標系(圖4).考察范圍到A、B兩點的距離之和不超過10km的區域.
(I)求考察區域邊界曲線的方程:
(II)如圖4所示,設線段![]() 是冰川的部分邊界線(不考慮其他邊界),當冰川融化時,邊界線沿與其垂直的方向朝考察區域平行移動,第一年移動0.2km,以后每年移動的距離為前一年的2倍.問:經過多長時間,點A恰好在冰川邊界線上?
是冰川的部分邊界線(不考慮其他邊界),當冰川融化時,邊界線沿與其垂直的方向朝考察區域平行移動,第一年移動0.2km,以后每年移動的距離為前一年的2倍.問:經過多長時間,點A恰好在冰川邊界線上?
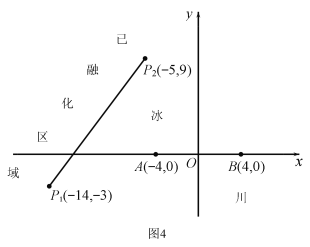
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,橢圓上一點
,橢圓上一點![]() 與
與![]() ,
,![]() 的距離之和為
的距離之和為![]() ,且焦距是短軸長的2倍.
,且焦距是短軸長的2倍.
(1)求橢圓的方程;
(2)過線段![]() 上一點的直線
上一點的直線![]() (斜率不為0)與橢圓相交于
(斜率不為0)與橢圓相交于![]() ,
,![]() 兩點,當
兩點,當![]() 的面積與
的面積與![]() 的面積之比為
的面積之比為![]() 時,求
時,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國高鐵的快速發展給群眾出行帶來巨大便利,極大促進了區域經濟社會發展.已知某條高鐵線路通車后,發車時間間隔![]() (單位:分鐘)滿足
(單位:分鐘)滿足![]() ,
,![]() ,經測算,高鐵的載客量與發車時間間隔
,經測算,高鐵的載客量與發車時間間隔![]() 相關:當
相關:當![]() 時高鐵為滿載狀態,載客量為1000人;當
時高鐵為滿載狀態,載客量為1000人;當![]() 時,載客量會在滿載基礎上減少,減少的人數與
時,載客量會在滿載基礎上減少,減少的人數與![]() 成正比,且發車時間間隔為5分鐘時的載客量為100人.記發車間隔為
成正比,且發車時間間隔為5分鐘時的載客量為100人.記發車間隔為![]() 分鐘時,高鐵載客量為
分鐘時,高鐵載客量為![]() .
.
(1)求![]() 的表達式;
的表達式;
(2)若該線路發車時間間隔為![]() 分鐘時的凈收益
分鐘時的凈收益![]() (元),當發車時間間隔為多少時,單位時間的凈收益
(元),當發車時間間隔為多少時,單位時間的凈收益![]() 最大?
最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com