
【題目】已知函數(shù)f(x)=2sin(x+ ![]() )cosx.
)cosx.
(1)若0≤x≤ ![]() ,求函數(shù)f(x)的值域;
,求函數(shù)f(x)的值域;
(2)設(shè)△ABC的三個(gè)內(nèi)角A,B,C所對(duì)的邊分別為a,b,c,若A為銳角且f(A)= ![]() ,b=2,c=3,求cos(A﹣B)的值.
,b=2,c=3,求cos(A﹣B)的值.
【答案】
(1)解:f(x)=2sin(x+ ![]() )cosx
)cosx
=(sinx+ ![]() cosx)cosx
cosx)cosx
=sinxcosx+ ![]() cos2x
cos2x
= ![]() sin2x+
sin2x+ ![]() cos2x+
cos2x+ ![]()
=sin(2x+ ![]() )+
)+ ![]() ;
;
由 ![]() 得,
得, ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
即函數(shù)f(x)的值域?yàn)?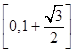
(2)解:由 ![]() ,
,
得 ![]() ,
,
又由 ![]() ,∴
,∴ ![]() ,
,
∴ ![]() ,解得
,解得 ![]() ;
;
在△ABC中,由余弦定理a2=b2+c2﹣2bccosA=7,
解得 ![]() ;
;
由正弦定理 ![]() ,得
,得 ![]() ,
,
∵b<a,∴B<A,∴ ![]() ,
,
∴cos(A﹣B)=cosAcosB+sinAsinB
= ![]()
【解析】(1)利用三角恒等變換化簡f(x),根據(jù)x的取值范圍即可求出函數(shù)f(x)的值域;(2)由f(A)的值求出角A的大小,再利用余弦定理和正弦定理,即可求出cos(A﹣B)的值.


 新課標(biāo)快樂提優(yōu)暑假作業(yè)陜西旅游出版社系列答案
新課標(biāo)快樂提優(yōu)暑假作業(yè)陜西旅游出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)y=f(x)的導(dǎo)函數(shù)y=f'(x)的圖象如圖所示,給出如下命題:
①0是函數(shù)y=f(x)的一個(gè)極值點(diǎn);
②函數(shù)y=f(x)在 ![]() 處切線的斜率小于零;
處切線的斜率小于零;
③f(﹣1)<f(0);
④當(dāng)﹣2<x<0時(shí),f(x)>0.
其中正確的命題是 . (寫出所有正確命題的序號(hào))
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若函數(shù)f(x)=|x﹣1|+m|x﹣2|+6|x﹣3|在x=2時(shí)取得最小值,則實(shí)數(shù)m的取值范圍是 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知?jiǎng)狱c(diǎn)![]() 到定點(diǎn)
到定點(diǎn)![]() 和
和![]() 的距離之和為
的距離之和為![]() .
.
(1)求動(dòng)點(diǎn)![]() 軌跡
軌跡![]() 的方程;
的方程;
(2)設(shè)![]() ,過點(diǎn)
,過點(diǎn)![]() 作直線
作直線![]() ,交橢圓
,交橢圓![]() 于不同于
于不同于![]() 的
的![]() 兩點(diǎn),直線
兩點(diǎn),直線![]() ,
, ![]() 的斜率分別為
的斜率分別為![]() ,
, ![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)是定義在[1,+∞)上的函數(shù),且f(x)=  ,則函數(shù)y=2xf(x)﹣3在區(qū)間(1,2016)上的零點(diǎn)個(gè)數(shù)為
,則函數(shù)y=2xf(x)﹣3在區(qū)間(1,2016)上的零點(diǎn)個(gè)數(shù)為
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù) ![]() ,其中a∈R.
,其中a∈R.
(1)根據(jù)a的不同取值,討論f(x)的奇偶性,并說明理由;
(2)已知a>0,函數(shù)f(x)的反函數(shù)為f﹣1(x),若函數(shù)y=f(x)+f﹣1(x)在區(qū)間[1,2]上的最小值為1+log23,求函數(shù)f(x)在區(qū)間[1,2]上的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】等差數(shù)列{an}的公差d≠0滿足![]() 成等比數(shù)列,若
成等比數(shù)列,若![]() =1,Sn是{
=1,Sn是{![]() }的前n項(xiàng)和,則
}的前n項(xiàng)和,則![]() 的最小值為________.
的最小值為________.
【答案】4
【解析】
![]() 成等比數(shù)列,
成等比數(shù)列,![]() =1,可得:
=1,可得:![]() =
=![]()
![]() ,即(1+2d)2=1+12d,d≠0,解得d.可得an,Sn.代入
,即(1+2d)2=1+12d,d≠0,解得d.可得an,Sn.代入![]() 利用分離常數(shù)法化簡后,利用基本不等式求出式子的最小值.
利用分離常數(shù)法化簡后,利用基本不等式求出式子的最小值.
∵![]() 成等比數(shù)列,a1=1,
成等比數(shù)列,a1=1,
∴![]() =
=![]()
![]() ,
,
∴(1+2d)2=1+12d,d≠0,
解得d=2.
∴an=1+2(n﹣1)=2n﹣1.
Sn=n+![]() ×2=n2.
×2=n2.
∴![]() =
=![]() =n+1+
=n+1+![]() ﹣2≥2
﹣2≥2![]() ﹣2=4,
﹣2=4,
當(dāng)且僅當(dāng)n+1=![]() 時(shí)取等號(hào),此時(shí)n=2,且
時(shí)取等號(hào),此時(shí)n=2,且![]() 取到最小值4,
取到最小值4,
故答案為:4.
【點(diǎn)睛】
本題考查了等差數(shù)列的通項(xiàng)公式、前n項(xiàng)和公式,等比中項(xiàng)的性質(zhì),基本不等式求最值,在利用基本不等式求最值時(shí),要特別注意“拆、拼、湊”等技巧,使其滿足基本不等式中“正”(即條件要求中字母為正數(shù))、“定”(不等式的另一邊必須為定值)、“等”(等號(hào)取得的條件)的條件才能應(yīng)用,否則會(huì)出現(xiàn)錯(cuò)誤.
【題型】填空題
【結(jié)束】
17
【題目】設(shè)![]() 是公比為正數(shù)的等比數(shù)列,
是公比為正數(shù)的等比數(shù)列,![]() ,
,![]()
(1)求![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)設(shè)![]() 是首項(xiàng)為1,公差為2的等差數(shù)列,求數(shù)列
是首項(xiàng)為1,公差為2的等差數(shù)列,求數(shù)列![]() 的前
的前![]() 項(xiàng)和
項(xiàng)和![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知公差不為0的等差數(shù)列{an}中,a1=2,且a2+1,a4+1,a8+1成等比數(shù)列.
(1)求數(shù)列{an}通項(xiàng)公式;
(2)設(shè)數(shù)列{bn}滿足bn= ![]() ,求適合方程b1b2+b2b3+…+bnbn+1=
,求適合方程b1b2+b2b3+…+bnbn+1= ![]() 的正整數(shù)n的值.
的正整數(shù)n的值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com