
【題目】某科研機構研發了某種高新科技產品,現已進入實驗階段.已知實驗的啟動資金為10萬元,從實驗的第一天起連續實驗,第![]() 天的實驗需投入實驗費用為
天的實驗需投入實驗費用為![]() 元
元![]() ,實驗30天共投入實驗費用17700元.
,實驗30天共投入實驗費用17700元.
(1)求![]() 的值及平均每天耗資最少時實驗的天數;
的值及平均每天耗資最少時實驗的天數;
(2)現有某知名企業對該項實驗進行贊助,實驗![]() 天共贊助
天共贊助![]() 元
元![]() .為了保證產品質量,至少需進行50天實驗,若要求在平均每天實際耗資最小時結束實驗,求
.為了保證產品質量,至少需進行50天實驗,若要求在平均每天實際耗資最小時結束實驗,求![]() 的取值范圍.(實際耗資=啟動資金+試驗費用-贊助費)
的取值范圍.(實際耗資=啟動資金+試驗費用-贊助費)
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
試題分析:(1)實驗開始后,每天的試驗費用構成公差為![]() ,首項為
,首項為![]() 的等差數列,通過等差數列的求和公式計算出這
的等差數列,通過等差數列的求和公式計算出這![]() 天所投入的試驗費用,然后便可求出
天所投入的試驗費用,然后便可求出![]() 的值,再利用等差數列的求和公式求出
的值,再利用等差數列的求和公式求出![]() 天內總計的試驗費用,然后再求出每天的平均試驗費用,利用基本不等式便可求出平均每天耗資最少時試驗的天數;(2)先求出實際耗資的連續函數,
天內總計的試驗費用,然后再求出每天的平均試驗費用,利用基本不等式便可求出平均每天耗資最少時試驗的天數;(2)先求出實際耗資的連續函數,![]() ,討論
,討論![]() 和
和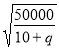 的大小關系即可解得
的大小關系即可解得![]() 的取值范圍為
的取值范圍為![]() .
.
試題解析:(1)依題意得,試驗開始后,每天的試驗費用構成等差數列,公差為![]() ,首項為
,首項為![]() ,
,
∴試驗30天共花費試驗費用為![]() ,
,
解得,![]() .............................2分
.............................2分
設試驗![]() 天,平均每天耗資為
天,平均每天耗資為![]() 元,則
元,則
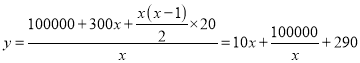 ..................4分
..................4分
![]() ,
,
當且僅當![]() ,即
,即![]() 時取等號,
時取等號,
綜上得,![]() ,試驗天數為100天..................................6分
,試驗天數為100天..................................6分
(2)設平均每天實際耗資為![]() 元,則
元,則
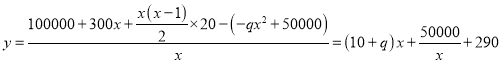 ...........8分
...........8分
當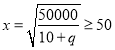 ,即
,即![]() 時,
時,
![]() ,因為
,因為![]() ,
,
所以,![]() ,.......................10分
,.......................10分
當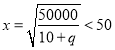 ,即
,即![]() 時,當
時,當![]() 時,
時,![]() 取最小值,
取最小值,
且![]() ,
,
綜上得,![]() 的取值范圍為
的取值范圍為![]() ....................12分
....................12分


科目:高中數學 來源: 題型:
【題目】已知關于x的一元二次函數![]() ,分別從集合P和Q中隨機取一個數a和b得到數對
,分別從集合P和Q中隨機取一個數a和b得到數對![]() 。
。
(1)若![]() ,
,![]() ,求函數
,求函數![]() 在
在![]() 內是偶函數的概率;
內是偶函數的概率;
(2)若![]() ,
,![]() ,求函數
,求函數![]() 有零點的概率;
有零點的概率;
(3)若![]() ,
,![]() ,求函數
,求函數![]() 在區間
在區間![]() 上是增函數的概率。
上是增函數的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 、
、![]() 分別是橢圓
分別是橢圓![]() 的左頂點、右焦點,點
的左頂點、右焦點,點![]() 為橢圓
為橢圓![]() 上一動點,當
上一動點,當![]() 軸時,
軸時, ![]() .
.
(1)求橢圓![]() 的離心率;
的離心率;
(2)若橢圓![]() 存在點
存在點![]() ,使得四邊形
,使得四邊形![]() 是平行四邊形(點
是平行四邊形(點![]() 在第一象限),求直線
在第一象限),求直線![]() 與
與![]() 的斜率之積;
的斜率之積;
(3)記圓![]() 為橢圓
為橢圓![]() 的“關聯圓”. 若
的“關聯圓”. 若![]() ,過點
,過點![]() 作橢圓
作橢圓![]() 的“關聯圓”的兩條切線,切點為
的“關聯圓”的兩條切線,切點為![]() 、
、![]() ,直線
,直線![]() 的橫、縱截距分別為
的橫、縱截距分別為![]() 、
、![]() ,求證:
,求證: ![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a,b,c為△ABC的三個內角A,B,C的對邊,向量![]() =(
=(![]() , ﹣1),
, ﹣1),![]() =(cosA,sinA).若
=(cosA,sinA).若![]() ⊥
⊥![]() , 且αcosB+bcosA=csinC,則角A,B的大小分別為( )
, 且αcosB+bcosA=csinC,則角A,B的大小分別為( )
A.![]() ,
,![]()
B.![]() ,
,![]()
C.![]() ,
,![]()
D.![]() ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面四邊形ABCD中,△BCD是正三角形,AB=AD=1,∠BAD=θ.
(Ⅰ)將四邊形ABCD的面積S表示成關于θ的函數;
(Ⅱ)求S的最大值及此時θ的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分,(1)小問7分,(2)小問5分)
設函數![]()
(1)若![]() 在
在![]() 處取得極值,確定
處取得極值,確定![]() 的值,并求此時曲線
的值,并求此時曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)若![]() 在
在![]() 上為減函數,求
上為減函數,求![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com