
【題目】在平面直角坐標系xOy中,已知拋物線C:![]() 的焦點為F,過F的直線
的焦點為F,過F的直線![]() 交拋物線C于A,B兩點.
交拋物線C于A,B兩點.
(1)求線段AF的中點M的軌跡方程;
(2)已知△AOB的面積是△BOF面積的3倍,求直線![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)設線段AF的中點的坐標為![]() ,
,![]() ,即可求得
,即可求得![]() ,將它們代入
,將它們代入![]() 即可得解。
即可得解。
(2)設![]() ,由△AOB的面積是△BOF面積的3倍可得:直線
,由△AOB的面積是△BOF面積的3倍可得:直線![]() 的斜率存在,且
的斜率存在,且![]() 的面積是
的面積是![]() 面積的2倍,即可整理得:
面積的2倍,即可整理得:![]() ,設直線
,設直線![]() 的方程為:
的方程為:![]() ,聯立直線方程與拋物線方程可得:
,聯立直線方程與拋物線方程可得:![]() ,
,![]() ,結合
,結合![]() 即可求得:
即可求得:![]() ,問題得解。
,問題得解。
(1)設線段AF的中點的坐標為![]() ,
,![]()
由拋物線![]() 的方程
的方程![]() 可得:焦點
可得:焦點![]()
由中點坐標公式可得:![]()
即:![]()
又![]() 在拋物線
在拋物線![]() 上,所以
上,所以![]() ,
,
將![]() 代入上式可得:
代入上式可得:![]()
整理得:![]()
所以線段AF的中點M的軌跡方程為:![]()
(2)依據題意作出圖形,如下:
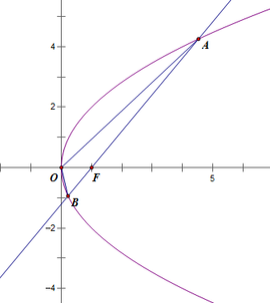
設![]() ,且
,且![]() 與
與![]() 的取值一正、一負
的取值一正、一負
因為△AOB的面積是△BOF面積的3倍,所以直線![]() 的斜率存在,
的斜率存在,
且![]() 的面積是
的面積是![]() 面積的2倍,
面積的2倍,
即:![]() ,整理得:
,整理得:![]()
設直線![]() 的方程為:
的方程為:![]()
聯立直線與拋物線方程可得:![]() ,整理得:
,整理得:![]() .
.
所以![]() ,
,![]()
由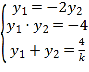 解得:
解得:![]() .
.
所以直線![]() 的方程為:
的方程為:![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】某市場研究人員為了了解產業園引進的甲公司前期的經營狀況,采集相應數據,對該公司2017年連續六個月的利潤進行了統計,并繪制了相應的折線圖,如圖所示:
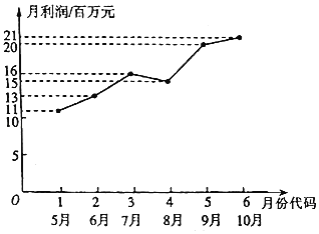
(1)折線圖可以看出,可用線性回歸模型擬合月利潤![]() (單位:百萬元)與月份代碼
(單位:百萬元)與月份代碼![]() 之間的關系,求
之間的關系,求![]() 關于
關于![]() 的線性回歸方程,并預測該公司2018年1月份的利潤;
的線性回歸方程,并預測該公司2018年1月份的利潤;
(2)甲公司新研制了一款產品,需要采購一批新型材料,現有采購成本分別為10萬元![]() 包和12萬元
包和12萬元![]() 包的
包的![]() 、
、![]() 兩種型號的新型材料可供選擇,按規定每種新型材料最多可使用4個月,不同類型的新型材料損壞的時間各不相同,已知生產新型材料的企業乙對
兩種型號的新型材料可供選擇,按規定每種新型材料最多可使用4個月,不同類型的新型材料損壞的時間各不相同,已知生產新型材料的企業乙對![]() 、
、![]() 兩種型號各100件新型材料進行過科學模擬測試,得到兩種新型材料使用壽命頻數統計如表:
兩種型號各100件新型材料進行過科學模擬測試,得到兩種新型材料使用壽命頻數統計如表:
使用壽命 材料類型 | 1個月 | 2個月 | 3個月 | 4個月 | 總計 |
| 20 | 35 | 35 | 10 | 100 |
| 10 | 30 | 40 | 20 | 100 |
經甲公司測算,平均每包新型材料每月可以帶來5萬元收入,不考慮除采購成本之外的其他成本,假設每包新型材料的使用壽命都是整數月,且以頻率作為每包新型材料使用壽命的概率,如果你是甲公司的負責人,以每包新型材料產生利潤的期望值為決策依據,你會選擇采購哪款新型材料?
參考數據:![]() ,
,![]() .
.
參考公式:回歸直線方程為![]() ,其中
,其中 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,曲線C:x2=6y與直線l:y=kx+3交于M,N兩點.
(1)設M,N到y軸的距離分別為d1,d2,證明:d1d2為定值.
(2)y軸上是否存在點P,使得當k變動時,總有∠OPM=∠OPN?若存在,求以線段OP為直徑的圓的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】京劇是我國的國粹,是“國家級非物質文化遺產”,為紀念著名京劇表演藝術家,京劇藝術大師梅蘭芳先生,某電視臺《我愛京劇》的一期比賽中,2位“梅派”傳人和4位京劇票友(資深業余愛好者)在幕后登臺演唱同一曲目《貴妃醉酒》選段,假設6位演員的演唱水平相當,由現場40位大眾評委和“梅派”傳人的朋友猜測哪兩位是真正的“梅派”傳人.
(1)此欄目編導對本期的40位大眾評委的年齡和對京劇知識的了解進行調查,根據調查得到的數據如下:
京劇票友 | 一般愛好者 | 合計 | |
50歲以上 | 15 | 10 | 25 |
50歲以下 | 3 | 12 | 15 |
合計 | 18 | 22 | 40 |
試問:在犯錯誤的概率不超過多少的前提下,可以認為年齡的大小與對京劇知識的了解有關系?
(2)若在一輪中演唱中,每猜出一位亮相一位,且規定猜出2位“梅派”傳人”或猜出5人后就終止,記本輪競猜一共競猜![]() 次,求隨機變量
次,求隨機變量![]() 的分布列與期望.
的分布列與期望.
參考數據:
0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
0.455 | 0.708 | 1.323 | 2.072 | 2.706 |
0.05 | 0.025 | 0.005 | 0.001 | |
3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
參考公式:![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點為
的左、右焦點為![]() ,左右兩頂點
,左右兩頂點![]() ,點
,點![]() 為橢圓
為橢圓![]() 上任意一點,滿足直線
上任意一點,滿足直線![]() 的斜率之積為
的斜率之積為![]() ,且
,且![]() 的最大值為4.
的最大值為4.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)已知直線![]() 與
與![]() 軸的交點為
軸的交點為![]() ,過
,過![]() 點的直線
點的直線![]() 與橢圓
與橢圓![]() 相交與
相交與![]() 兩點,連接點
兩點,連接點![]() 并延長,交軌跡
并延長,交軌跡![]() 于一點
于一點![]() .求證:
.求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圖1是由正方形![]() ,直角梯形
,直角梯形![]() ,三角形
,三角形![]() 組成的一個平面圖形,其中
組成的一個平面圖形,其中![]() ,
,![]() ,將其沿
,將其沿![]() ,
,![]() 折起使得
折起使得![]() 與
與![]() 重合,連接
重合,連接![]() ,如圖2.
,如圖2.
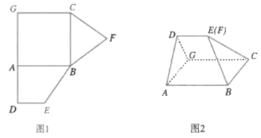
(1)證明:圖2中的![]() ,
,![]() ,
,![]() ,
,![]() 四點共面,且平面
四點共面,且平面![]() 平面
平面![]() ;
;
(2)求圖2中的點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某保險公司對一個擁有20000人的企業推出一款意外險產品,每年每位職工只要交少量保費,發生意外后可一次性獲得若干賠償金,保險公司把企業的所有崗位共分為![]() 三類工種,從事這三類工種的人數分別為12000,6000,2000,由歷史數據統計出三類工種的賠付頻率如下表(并以此估計賠付概率):
三類工種,從事這三類工種的人數分別為12000,6000,2000,由歷史數據統計出三類工種的賠付頻率如下表(并以此估計賠付概率):
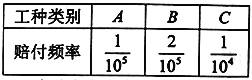
已知![]() 三類工種職工每人每年保費分別為25元、25元、40元,出險后的賠償金額分別為100萬元、100萬元、50萬元,保險公司在開展此項業務過程中的固定支出為每年10萬元.
三類工種職工每人每年保費分別為25元、25元、40元,出險后的賠償金額分別為100萬元、100萬元、50萬元,保險公司在開展此項業務過程中的固定支出為每年10萬元.
(1)求保險公司在該業務所或利潤的期望值;
(2)現有如下兩個方案供企業選擇:
方案1:企業不與保險公司合作,職工不交保險,出意外企業自行拿出與保險公司提供的等額賠償金賠償付給意外職工,企業開展這項工作的固定支出為每年12萬元;
方案2:企業與保險公司合作,企業負責職工保費的70%,職工個人負責保費的30%,出險后賠償金由保險公司賠付,企業無額外專項開支.
請根據企業成本差異給出選擇合適方案的建議.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A(0,2),動點M到點A的距離比動點M到直線y=﹣1的距離大1,動點M的軌跡為曲線C.
(1)求曲線C的方程;
(2)Q為直線y=﹣1上的動點,過Q做曲線C的切線,切點分別為D、E,求△QDE的面積S的最小值
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com