
【題目】已知![]() (
(![]() ,且
,且![]() ).
).
(1)當(dāng)![]() (其中
(其中![]() ,且t為常數(shù))時(shí),
,且t為常數(shù))時(shí),![]() 是否存在最小值,如果存在,求出最小值;如果不存在,請說明理由;
是否存在最小值,如果存在,求出最小值;如果不存在,請說明理由;
(2)當(dāng)![]() 時(shí),求滿足不等式
時(shí),求滿足不等式![]() 的實(shí)數(shù)x的取值范圍.
的實(shí)數(shù)x的取值范圍.
【答案】(1)見解析(2)![]()
【解析】
(1)先判定函數(shù)的單調(diào)性,結(jié)合單調(diào)性來進(jìn)行求解![]() 是否存在最小值;
是否存在最小值;
(2)先判斷函數(shù)的奇偶性及單調(diào)性,結(jié)合奇偶性和單調(diào)性把![]() 進(jìn)行轉(zhuǎn)化求解.
進(jìn)行轉(zhuǎn)化求解.
(1)由![]() 可得
可得![]() 或
或![]() ,解得
,解得![]() ,即函數(shù)
,即函數(shù)![]() 的定義域?yàn)?/span>
的定義域?yàn)?/span>![]() ,
,
設(shè)![]() ,則
,則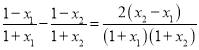 ,∵
,∵![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() ,
,
①當(dāng)![]() 時(shí)
時(shí)![]() ,則
,則![]() 在
在![]() 上是減函數(shù),又
上是減函數(shù),又![]() ,
,
∴![]() 時(shí),
時(shí),![]() 有最小值,且最小值為
有最小值,且最小值為![]() ;
;
②當(dāng)![]() 時(shí),
時(shí),![]() ,則
,則![]() 在
在![]() 上是增函數(shù),又
上是增函數(shù),又![]() ,
,
∴![]() 時(shí),
時(shí),![]() 無最小值.
無最小值.
(2)由于![]() 的定義域?yàn)?/span>
的定義域?yàn)?/span>![]() ,定義域關(guān)于原點(diǎn)對稱,且
,定義域關(guān)于原點(diǎn)對稱,且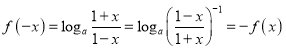 ,所以函數(shù)
,所以函數(shù)![]() 為奇函數(shù).由(1)可知,當(dāng)
為奇函數(shù).由(1)可知,當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 為減函數(shù),由此,不等式
為減函數(shù),由此,不等式![]() 等價(jià)于
等價(jià)于![]() ,即有
,即有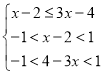 ,解得
,解得![]() ,所以x的取值范圍是
,所以x的取值范圍是![]() .
.


 鴻圖圖書寒假作業(yè)假期作業(yè)吉林大學(xué)出版社系列答案
鴻圖圖書寒假作業(yè)假期作業(yè)吉林大學(xué)出版社系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某種設(shè)備隨著使用年限的增加,每年的維護(hù)費(fèi)相應(yīng)增加.現(xiàn)對一批該設(shè)備進(jìn)行調(diào)查,得到這批設(shè)備自購入使用之日起,前5年平均每臺(tái)設(shè)備每年的維護(hù)費(fèi)用大致如表:
年份 |
|
|
|
|
|
維護(hù)費(fèi) |
|
|
|
|
|
已知![]() .
.
(I)求表格中![]() 的值;
的值;
(II)從這![]() 年中隨機(jī)抽取兩年,求平均每臺(tái)設(shè)備每年的維護(hù)費(fèi)用至少有
年中隨機(jī)抽取兩年,求平均每臺(tái)設(shè)備每年的維護(hù)費(fèi)用至少有![]() 年多于
年多于![]() 萬元的概率;
萬元的概率;
(Ⅲ)求![]() 關(guān)于
關(guān)于![]() 的線性回歸方程;并據(jù)此預(yù)測第幾年開始平均每臺(tái)設(shè)備每年的維護(hù)費(fèi)用超過
的線性回歸方程;并據(jù)此預(yù)測第幾年開始平均每臺(tái)設(shè)備每年的維護(hù)費(fèi)用超過![]() 萬元.
萬元.
參考公式:用最小二乘法求線性回歸方程![]() 的系數(shù)公式:
的系數(shù)公式:
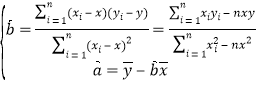
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
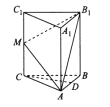
【題目】如圖,在三棱柱![]() 中,側(cè)棱
中,側(cè)棱![]() 底面
底面![]() ,且
,且![]() ,
, ![]() 是棱
是棱![]() 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)![]() 在側(cè)棱
在側(cè)棱![]() 上運(yùn)動(dòng).
上運(yùn)動(dòng).
(1)當(dāng)![]() 是棱
是棱![]() 的中點(diǎn)時(shí),求證:
的中點(diǎn)時(shí),求證: ![]() 平面
平面![]() ;
;
(2)當(dāng)直線![]() 與平面
與平面![]() 所成的角的正切值為
所成的角的正切值為![]() 時(shí),求二面角
時(shí),求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2018年5月21日5點(diǎn)28分,在我國西昌衛(wèi)星發(fā)射中心,由中國航天科技集團(tuán)有限公司抓總研制的嫦娥四號中繼星“鵲橋”搭乘長征四號丙運(yùn)載火箭升空,這標(biāo)志著我國在月球探測領(lǐng)域取得新的突破.早在1671年,兩位法國天文學(xué)家就已經(jīng)成功測量出了地球與月球之間的距離,接下來,讓我們重走這兩位科學(xué)家的測量過程.如圖,設(shè)O為地球球心,C為月球表面上一點(diǎn),A,B為地球上位于同一子午線(經(jīng)線)上的兩點(diǎn),地球半徑記為R.

步驟一:經(jīng)測量,A,B兩點(diǎn)的緯度分別為北緯![]() 和南緯
和南緯![]() ,即
,即![]() ,可求得
,可求得![]() ;
;
步驟二:經(jīng)測量計(jì)算,![]() ,
,![]() ,計(jì)算
,計(jì)算![]() ;
;
步驟三:利用以上測量及計(jì)算結(jié)果,計(jì)算![]() .
.
請你用解三角形的相關(guān)知識,求出步驟二三中的![]() 及
及![]() 的值(結(jié)果均用
的值(結(jié)果均用![]() ,
,![]() ,R表示).
,R表示).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某地下車庫在排氣扇發(fā)生故障的情況下,測得空氣中一氧化碳含量達(dá)到了危險(xiǎn)狀態(tài),經(jīng)搶修,排氣扇恢復(fù)正常.排氣![]() 后,測得車庫內(nèi)的一氧化碳濃度為
后,測得車庫內(nèi)的一氧化碳濃度為![]() ,繼續(xù)排氣
,繼續(xù)排氣![]() ,又測得濃度為
,又測得濃度為![]() ,經(jīng)檢測知該地下車庫一氧化碳濃度
,經(jīng)檢測知該地下車庫一氧化碳濃度![]() 與排氣時(shí)間
與排氣時(shí)間![]() 存在函數(shù)關(guān)系:
存在函數(shù)關(guān)系: (
(![]() ,
,![]() 為常數(shù))。
為常數(shù))。
(1)求![]() ,
,![]() 的值;
的值;
(2)若地下車庫中一氧化碳濃度不高于![]() 為正常,問至少排氣多少分鐘,這個(gè)地下車庫中的一氧化碳含量才能達(dá)到正常狀態(tài)?
為正常,問至少排氣多少分鐘,這個(gè)地下車庫中的一氧化碳含量才能達(dá)到正常狀態(tài)?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如果函數(shù)![]() 在定義域的某個(gè)區(qū)間
在定義域的某個(gè)區(qū)間![]() 上的值域恰為
上的值域恰為![]() ,則稱函數(shù)
,則稱函數(shù)![]() 為
為![]() 上的等域函數(shù),
上的等域函數(shù),![]() 稱為函數(shù)
稱為函數(shù)![]() 的一個(gè)等域區(qū)間.
的一個(gè)等域區(qū)間.
(1)若函數(shù)![]() ,
,![]() ,則函數(shù)
,則函數(shù)![]() 存在等域區(qū)間嗎?若存在,試寫出其一個(gè)等域區(qū)間,若不存在,說明理由
存在等域區(qū)間嗎?若存在,試寫出其一個(gè)等域區(qū)間,若不存在,說明理由
(2)已知函數(shù)![]() ,其中
,其中![]() 且
且![]() ,
,![]() ,
,![]() .
.
(ⅰ)當(dāng)![]() 時(shí),若函數(shù)
時(shí),若函數(shù)![]() 是
是![]() 上的等域函數(shù),求
上的等域函數(shù),求![]() 的解析式;
的解析式;
(ⅱ)證明:當(dāng)![]() ,
,![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 不存在等域區(qū)間.
不存在等域區(qū)間.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】給出下列五個(gè)命題,其中正確的命題序號是________.
①當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 取得最大值,則
取得最大值,則![]()
②已知菱形![]() ,
,![]() 為
為![]() 的中點(diǎn),且
的中點(diǎn),且![]() ,則菱形
,則菱形![]() 面積的最大值為12
面積的最大值為12
③已知二次函數(shù)![]() ,如果
,如果![]() 時(shí)
時(shí)![]() ,則實(shí)數(shù)
,則實(shí)數(shù)![]() 的取值范圍是
的取值范圍是![]()
④在三棱錐![]() 中,
中,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 分別是
分別是![]() 的中點(diǎn),則異面直線
的中點(diǎn),則異面直線![]() 所成的角的余弦值是
所成的角的余弦值是![]()
⑤數(shù)列![]() 滿足
滿足![]() ,且數(shù)列
,且數(shù)列![]() 的前2010項(xiàng)的和為403,記數(shù)列
的前2010項(xiàng)的和為403,記數(shù)列![]() ,
,![]() 是數(shù)列
是數(shù)列![]() 的前
的前![]() 項(xiàng)和,則
項(xiàng)和,則![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=ax2-2x+1.
(1)試討論函數(shù)f(x)的單調(diào)性;
(2)若![]() ≤a≤1,且f(x)在[1,3]上的最大值為M(a),最小值為N(a),令g(a)=M(a)-N(a),求g(a)的表達(dá)式;
≤a≤1,且f(x)在[1,3]上的最大值為M(a),最小值為N(a),令g(a)=M(a)-N(a),求g(a)的表達(dá)式;
(3)在(2)的條件下,求證:g(a)≥![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)三棱錐![]() 的底面是正三角形,側(cè)棱長均相等,
的底面是正三角形,側(cè)棱長均相等,![]() 是棱
是棱![]() 上的點(diǎn)(不含端點(diǎn)),記直線
上的點(diǎn)(不含端點(diǎn)),記直線![]() 與直線
與直線![]() 所成角為
所成角為![]() ,直線
,直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,二面角
,二面角![]() 的平面角為
的平面角為![]() ,則( )
,則( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com