【題目】設三棱錐
的底面是正三角形，側棱長均相等，
是棱
上的點（不含端點），記直線
與直線
所成角為
，直線與平面
所成角為
，二面角
的平面角為
，則（ ）
A. 
B. 
C. 
D. 
培優口算題卡系列答案
開心口算題卡系列答案
口算題卡河北少年兒童出版社系列答案科目：高中數學 來源： 題型：
【題目】已知
（
，且
）.
（1）當
（其中
，且t為常數）時，
是否存在最小值，如果存在，求出最小值；如果不存在，請說明理由；
（2）當
時，求滿足不等式
的實數x的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，直線
的參數方程為
（
為參數），在極坐標系中，圓C的極坐標方程為：
（1）求圓C的直角坐標方程；
（2）設圓C與直線交于
兩點，若點的坐標為
,求
的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某地區為了解群眾上下班共享單車使用情況，根據年齡按分層抽樣的方式調查了該地區50名群眾，他們的年齡頻數及使用共享單車人數分布如下表：
年齡段 | 20~29 | 30~39 | 40~49 | 50~60 |
頻數 | 12 | 18 | 15 | 5 |
經常使用共享單車 | 6 | 12 | 5 | 1 |
（1）由以上統計數據完成下面的
列聯表，并判斷是否有95%的把握認為以40歲為分界點對是否經常使用共享單車有差異？
年齡低于40歲 | 年齡不低于40歲 | 總計 | |
經常使用共享單車 | |||
不經常使用共享單車 | |||
總計 |
附：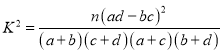
，
.
| 0.25 | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
（2）若采用分層抽樣的方式從年齡低于40歲且經常使用共享單車的群眾中選出6人，再從這6人中隨機抽取2人，求這2人中恰好有1人年齡在30~39歲的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
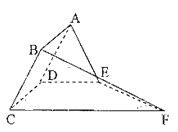
【題目】如圖，矩形
所在的半平面和直角梯形
所在的半平面成
的二面角，
，
，
，
，
，
.
（Ⅰ）求證：平面
平面
；
（Ⅱ）試問在線段
上是否存在一點
，使銳二面角
的余弦值為
.若存在，請求出
的值；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】圖1是由矩形
和菱形
組成的一個平面圖形，其中
， 
，將其沿
折起使得
與
重合，連結
，如圖2.
（1）證明圖2中的
四點共面，且平面
平面
；
（2）求圖2中的四邊形
的面積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在一個盒子中，放有標號分別為1，2，3的三張卡片，現從這個盒子中，有放回地先后抽得兩張卡片的標號分別為x、y，設O為坐標原點，點P的坐標為
記
.
（1）求隨機變量
的最大值，并求事件“取得最大值”的概率；
（2）求隨機變量的分布列和數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2015年推出一種新型家用轎車，購買時費用為16.9萬元，每年應交付保險費、養路費及汽油費共1.2萬元，汽車的維修費為：第一年無維修費用，第二年為0.2萬元，從第三年起，每年的維修費均比上一年增加0.2萬元.
（I）設該輛轎車使用n年的總費用（包括購買費用、保險費、養路費、汽油費及維修費）為f(n)，求f(n)的表達式；
（II）這種汽車使用多少報廢最合算（即該車使用多少年，年平均費用最少）？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
