【題目】已知雙曲線
過點
，且漸近線方程為
，直線
與曲線交于點
、
兩點.
（1）求雙曲線的方程；
（2）若直線過原點，點
是曲線上任一點，直線
，
的斜率都存在，記為
、
，試探究
的值是否與點及直線有關，并證明你的結論；
（3）若直線過點
，問在
軸上是否存在定點
，使得
為常數？若存在，求出點坐標及此常數的值；若不存在，說明理由.
【答案】（1）
；（2）
，
的值與點
及直線
無關，證明見解析；（3）存在，
， 
，理由見解析
【解析】
（1）根據漸近線設出漸近線方程，將點
代入即可求出雙曲線
的方程.
（2）根據直線與雙曲線的對稱性知道點
與點
關于原點對稱，設出點、、，將其斜率表示出來，利用點、在雙曲線上，化簡即可說明為定值且直線與關.
（3）根據題意設出直線與點
，聯立直線與雙曲線，表示出
，利用為定值，即與斜率無關，根據比值即可求出定點與的值.
（1） 因為漸近線方程為
.
所以可設雙曲線為
,
將點
代入
，解得
所以雙曲線的方程為
（2）直線過原點,由雙曲線的對稱性知道，點、關于原點對稱.
設點
，
，則點
代入，有
，
所以
，
.
將，代入得
.
所以，的值與點及直線無關.
（3）由題意知直線斜率存在，故設直線為
，點
、
、
由
，得 
，
且
又
，
，
所以
令
解得
，此時
培優好卷單元加期末卷系列答案科目：高中數學 來源： 題型：
【題目】某企業參加
項目生產的工人為
人，平均每人每年創造利潤
萬元.根據現實的需要，從項目中調出
人參與
項目的售后服務工作，每人每年可以創造利潤
萬元（
），項目余下的工人每人每年創造利圖需要提高
（1）若要保證項目余下的工人創造的年總利潤不低于原來名工人創造的年總利潤，則最多調出多少人參加項目從事售后服務工作？
（2）在（1）的條件下，當從項目調出的人數不能超過總人數的
時，才能使得項目中留崗工人創造的年總利潤始終不低于調出的工人所創造的年總利潤，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
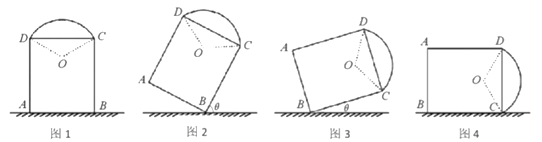
【題目】如圖1，一藝術拱門由兩部分組成，下部為矩形
的長分別為
米和
米，上部是圓心為
的劣弧
，
（1）求圖1中拱門最高點到地面的距離：
（2）現欲以
點為支點將拱門放倒，放倒過程中矩形
所在的平面始終與地面垂直，如圖2、圖3、圖4所示，設
與地面水平線
所成的角為
.若拱門上的點到地面的最大距離恰好為
到地面的距離，試求的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于給定的正整數
，若數列
滿足
對任意正整數
恒成立，則稱數列是
數列，若正數項數列
，滿足：
對任意正整數恒成立，則稱是
數列；
（1）已知正數項數列是
數列，且前五項分別為
、
、
、
、
，求的值；
（2）若
為常數，且是
數列，求
的最小值；
（3）對于下列兩種情形，只要選作一種，滿分分別是 ①
分，②
分，若選擇了多于一種情形，則按照序號較小的解答記分.
① 證明：數列是等差數列的充要條件為“既是數列，又是
數列”；
②證明：正數項數列是等比數列的充要條件為“數列既是
數列，又是
數列”.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列
的前6項依次成等比數列，設公比為q（
），數列從第5項開始各項依次為等差數列，其中
，數列的前n項和為
.
（1）求公比q及數列的通項公式；
（2）若
，求項數n的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】定義：若函數
對任意的
，都有
成立，則稱為
上的“淡泊”函數.
（1）判斷
是否為
上的“淡泊”函數，說明理由；
（2）是否存在實數
，使
為
上的“淡泊”函數，若存在，求出的取值范圍；不存在，說明理由；
（3）設是
上的“淡泊”函數（其中不是常值函數），且
，若對任意的
，都有
成立，求
的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】
已知函數f（x）=
，其中a>0.
（Ⅰ）若a=1，求曲線y=f（x）在點（2，f（2））處的切線方程；
（Ⅱ）若在區間
上，f（x）>0恒成立，求a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
