
【題目】已知函數![]() .
.
(1)當![]() 時,求
時,求![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)若函數![]() 在
在![]() 上單調遞增,求實數
上單調遞增,求實數![]() 的取值范圍;
的取值范圍;
(3)證明:當![]() 時,不等式
時,不等式![]() 成立.
成立.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)證明見解析
;(3)證明見解析
【解析】
(1)當![]() 時,
時,![]() ,
,![]() ,故切線為
,故切線為![]()
(2)由題意得:![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 恒成立,求
恒成立,求![]() 的最小值,即可得出答案.
的最小值,即可得出答案.
(3)當![]() 時,可證明
時,可證明![]() 恒成立,變形得:
恒成立,變形得:![]() ,
,
又因為![]() ,即
,即![]() ,故
,故![]() ,將
,將![]() 替換成
替換成![]() ,即可得出答案.
,即可得出答案.
解:(1)![]() 時,
時,![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,
∴切線方程為![]() .
.
(2)由題可知![]() 在
在![]() 上恒成立,
上恒成立,
∴![]() 恒成立,
恒成立,
設函數![]() ,則
,則![]() ,
,
令![]() 得
得![]() ,
,
當![]() 時
時![]() ,當
,當![]() 時
時![]() ,
,
∴![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 單調遞增,
單調遞增,
∴![]() .
.
∴![]() ,∴
,∴![]() 的取值范圍是
的取值范圍是![]() .
.
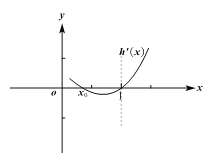
(3)首先證明:當![]() 時,
時,![]() .
.
設![]() ,則
,則![]() ,
,![]() .
.
易得:![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 單調遞增.
單調遞增.
又![]() ,
,![]() ,
,![]() ,∴
,∴![]() .
.
所以存在![]() 使得
使得![]() .
.
∴當![]() 時
時![]() ,當
,當![]() 時
時![]() ,
,
當![]() 時
時![]() .
.
∴![]() 在
在![]() ,
,![]() 單調遞增,在
單調遞增,在![]() 單調遞減,
單調遞減,
∵![]() ,∴
,∴![]() 在
在![]() 都成立,
都成立,
即![]() 時
時![]() 恒成立.
恒成立.
即:![]() ,變形得:
,變形得:![]() ,
,
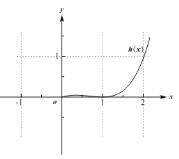
設![]() ,
,![]() ,
,![]() ,
,
∵當![]() 時,
時,![]() ,
,
當![]() 時,
時,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
將![]() 替換成
替換成![]() 得:
得:![]() .
.


科目:高中數學 來源: 題型:
【題目】“中國剩余定理”又稱“孫子定理”,最早可見于中國南北朝時期的數學著作《孫子算經》卷下第二十六題,叫做“物不知數”,原文如下:今有物不知其數,三三數之剩二,五五數之剩三,七七數之剩二.問物幾何?現有這樣一個相關的問題:將1到2020這2020個自然數中被5除余3且被7除余2的數按照從小到大的順序排成一列,構成一個數列,則該數列各項之和為( )
A.56383B.57171C.59189D.61242
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是一個單調遞增的等比數列,
是一個單調遞增的等比數列,![]() 是一個等差數列,
是一個等差數列,![]() 是
是![]() 的前
的前![]() 項和,其中
項和,其中![]() ,
,![]() ,
,![]() 成等差數列,
成等差數列,![]() .
.
(1)求![]() 的通項公式;
的通項公式;
(2)若![]() ,
,![]() ,
,![]() 既成等比數列,又成等差數列.
既成等比數列,又成等差數列.
(i)求![]() 的通項公式;
的通項公式;
(ii)對于數列![]() ,若
,若![]() 且
且![]() ,或
,或![]() 且
且![]() ,則
,則![]() 為數列
為數列![]() 的轉折點,求
的轉折點,求![]() 的轉折點個數.
的轉折點個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高三(1)班在一次語文測試結束后,發現同學們在背誦內容方面失分較為嚴重.為了提升背誦效果,班主任倡議大家在早晩讀時間站起來大聲誦讀,為了解同學們對站起來大聲誦讀的態度,對全班50名同學進行調查,將調查結果進行整理后制成如表:
考試分數 |
|
|
|
|
|
|
頻數 | 5 | 10 | 15 | 5 | 10 | 5 |
贊成人數 | 4 | 6 | 9 | 3 | 6 | 4 |
(1)欲使測試優秀率為![]() ,則優秀分數線應定為多少分?
,則優秀分數線應定為多少分?
(2)依據第1問的結果及樣本數據研究是否贊成站起來大聲誦讀的態度與考試成績是否優秀的關系,列出2×2列聯表,并判斷是否有![]() 的把握認為贊成與否的態度與成績是否優秀有關系.
的把握認為贊成與否的態度與成績是否優秀有關系.
參考公式及數據: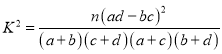 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 過點
過點![]() ,且與
,且與![]() 內切,設
內切,設![]() 的圓心
的圓心![]() 的軌跡為
的軌跡為![]() ,
,
(1)求軌跡C的方程;
(2)設直線![]() 不經過點
不經過點![]() 且與曲線
且與曲線![]() 交于點
交于點![]() 兩點,若直線
兩點,若直線![]() 與直線
與直線![]() 的斜率之積為
的斜率之積為![]() ,判斷直線
,判斷直線![]() 是否過定點,若過定點,求出此定點的坐標,若不過定點,請說明理由.
是否過定點,若過定點,求出此定點的坐標,若不過定點,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
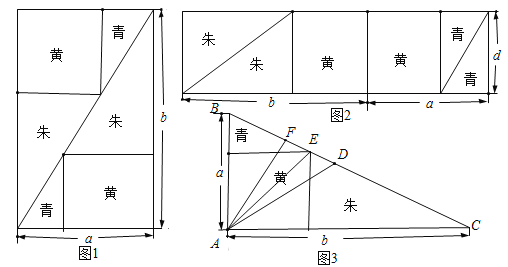
【題目】《九章算術》中“勾股容方”問題:“今有勾五步,股十二步,問勾中容方幾何?”魏晉時期數學家劉徽在其《九章算術注》中利用出入相補原理給出了這個問題的一般解法:如圖1,用對角線將長和寬分別為![]() 和
和![]() 的矩形分成兩個直角三角形,每個直角三角形再分成一個內接正方形(黃)和兩個小直角三角形(朱、青).將三種顏色的圖形進行重組,得到如圖2所示的矩形.該矩形長為
的矩形分成兩個直角三角形,每個直角三角形再分成一個內接正方形(黃)和兩個小直角三角形(朱、青).將三種顏色的圖形進行重組,得到如圖2所示的矩形.該矩形長為![]() ,寬為內接正方形的邊長
,寬為內接正方形的邊長![]() .由劉徽構造的圖形還可以得到許多重要的結論,如圖3.設
.由劉徽構造的圖形還可以得到許多重要的結論,如圖3.設![]() 為斜邊
為斜邊![]() 的中點,作直角三角形
的中點,作直角三角形![]() 的內接正方形對角線
的內接正方形對角線![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() ,則下列推理正確的是( )
,則下列推理正確的是( )
①由圖1和圖2面積相等得![]() ;
;
②由![]() 可得
可得![]() ;
;
③由![]() 可得
可得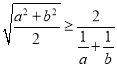 ;
;
④由![]() 可得
可得![]() .
.
A.①②③④B.①②④C.②③④D.①③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 在
在![]() 處取得極值A,函數
處取得極值A,函數![]() ,其中
,其中![]() …是自然對數的底數.
…是自然對數的底數.
(1)求m的值,并判斷A是![]() 的最大值還是最小值;
的最大值還是最小值;
(2)求![]() 的單調區間;
的單調區間;
(3)證明:對于任意正整數n,不等式![]() 成立.
成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)![]() (cosθ+1)cos2x+cosθ(cosx+1),有下述四個結論:①f(x)是偶函數;②f(x)在(
(cosθ+1)cos2x+cosθ(cosx+1),有下述四個結論:①f(x)是偶函數;②f(x)在(![]() ,
,![]() )上單調遞減;③當θ∈[
)上單調遞減;③當θ∈[![]() ,
,![]() ]時,有|f(x)|
]時,有|f(x)|![]() ;④當θ∈[
;④當θ∈[![]() ,
,![]() ]時,有|f'(x)|
]時,有|f'(x)|![]() ;其中所有真命題的編號是( )
;其中所有真命題的編號是( )
A.①③B.②④C.①③④D.①④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com