
【題目】已知橢圓C: ![]() =1(a>b>0),e=
=1(a>b>0),e= ![]() ,其中F是橢圓的右焦點,焦距為2,直線l與橢圓C交于點A、B,點A,B的中點橫坐標為
,其中F是橢圓的右焦點,焦距為2,直線l與橢圓C交于點A、B,點A,B的中點橫坐標為 ![]() ,且
,且 ![]() =λ
=λ ![]() (其中λ>1).
(其中λ>1).
(1)求橢圓C的標準方程;
(2)求實數λ的值.
【答案】
(1)解:由條件可知c=1,a=2,故b2=a2﹣c2=3,
橢圓的標準方程是 ![]() .
.
(2)解:由 ![]() ,可知A,B,F三點共線,設A(x1,y1),B(x2,y2),
,可知A,B,F三點共線,設A(x1,y1),B(x2,y2),
若直線AB⊥x軸,則x1=x2=1,不合題意.
當AB所在直線l的斜率k存在時,設方程為y=k(x﹣1).
由  ,消去y得(3+4k2)x2﹣8k2x+4k2﹣12=0.①
,消去y得(3+4k2)x2﹣8k2x+4k2﹣12=0.①
由①的判別式△=64k4﹣4(4k2+3)(4k2﹣12)=144(k2+1)>0.
因為  ,
,
所以 ![]() =
= ![]() ,所以
,所以 ![]() .
.
將 ![]() 代入方程①,得4x2﹣2x﹣11=0,
代入方程①,得4x2﹣2x﹣11=0,
解得x= ![]() .
.
又因為 ![]() =(1﹣x1,﹣y1),
=(1﹣x1,﹣y1), ![]() =(x2﹣1,y2),
=(x2﹣1,y2), ![]() ,
,
![]() ,解得
,解得 ![]()
【解析】(1)由條件可知c=1,a=2,由此能求出橢圓的標準方程.(2)由 ![]() ,可知A,B,F三點共線,設A(x1 , y1),B(x2 , y2),直線AB⊥x軸,則x1=x2=1,不合意題意.當AB所在直線l的斜率k存在時,設方程為y=k(x﹣1).由
,可知A,B,F三點共線,設A(x1 , y1),B(x2 , y2),直線AB⊥x軸,則x1=x2=1,不合意題意.當AB所在直線l的斜率k存在時,設方程為y=k(x﹣1).由  ,得(3+4k2)x2﹣8k2x+4k2﹣12=0,由此利用根的判別式、韋達定理,結合已知條件能求出實數λ的值.
,得(3+4k2)x2﹣8k2x+4k2﹣12=0,由此利用根的判別式、韋達定理,結合已知條件能求出實數λ的值.


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案科目:高中數學 來源: 題型:
【題目】在一次抽樣調查中測得樣本的6組數據,得到一個變量![]() 關于
關于![]() 的回歸方程模型,其對應的數值如下表:
的回歸方程模型,其對應的數值如下表:
| 2 | 3 | 4 | 5 | 6 | 7 |
|
|
|
|
|
|
|
(1)請用相關系數![]() 加以說明
加以說明![]() 與
與![]() 之間存在線性相關關系(當
之間存在線性相關關系(當![]() 時,說明
時,說明![]() 與
與![]() 之間具有線性相關關系);
之間具有線性相關關系);
(2)根據(1)的判斷結果,建立![]() 關于
關于![]() 的回歸方程并預測當
的回歸方程并預測當![]() 時,對應的
時,對應的![]() 值為多少(
值為多少(![]() 精確到
精確到![]() ).
).
附參考公式:回歸方程![]() 中斜率和截距的最小二乘法估計公式分別為:
中斜率和截距的最小二乘法估計公式分別為:
 ,
,![]() ,相關系數
,相關系數![]() 公式為:
公式為: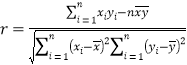 .
.
參考數據:
![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數![]() 的圖象上各點橫坐標縮短到原來的
的圖象上各點橫坐標縮短到原來的![]() (縱坐標不變)得到函數g(x)的圖象,則下列說法不正確的是()
(縱坐標不變)得到函數g(x)的圖象,則下列說法不正確的是()
A.函數g(x)的圖象關于點![]() 對稱
對稱
B.函數g(x)的周期是![]()
C.函數g(x)在![]() 上單調遞增
上單調遞增
D.函數g(x)在![]() 上最大值是1
上最大值是1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC中,AB=AC,D是△ABC外接圓上 ![]() 上的點(不與點A、C重合),延長BD至F.
上的點(不與點A、C重合),延長BD至F. 
(1)求證:AD延長線DF平分∠CDE;
(2)若∠BAC=30°,△ABC中BC邊上的高為2+ ![]() ,求△ABC外接圓的面積.
,求△ABC外接圓的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人各射擊一次,擊中目標的概率分別是![]() 和
和![]() .假設兩人射擊是否擊中目標,相互之間沒有影響;每次射擊是否擊中目標,相互之間沒有影響.
.假設兩人射擊是否擊中目標,相互之間沒有影響;每次射擊是否擊中目標,相互之間沒有影響.
(1)求甲射擊4次,至少1次未擊中目標的概率;
(2)求兩人各射擊4次,甲恰好擊中目標2次且乙恰好擊中目標3次的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,已知直線
中,已知直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點為極點,以
為參數),以坐標原點為極點,以![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點.
兩點.
(1)求直線![]() l的普通方程和曲線
l的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)已知點![]() 的極坐標為
的極坐標為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是函數![]() 的導函數
的導函數![]() 的圖象,給出下列命題:
的圖象,給出下列命題:

①-2是函數![]() 的極值點;
的極值點;
②![]() 是函數
是函數![]() 的極值點;
的極值點;
③![]() 在
在![]() 處取得極大值;
處取得極大值;
④函數![]() 在區間
在區間![]() 上單調遞增.則正確命題的序號是
上單調遞增.則正確命題的序號是
A. ①③ B. ②④ C. ②③ D. ①④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com