
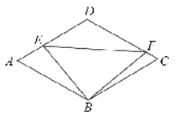
【題目】如圖,郊外有一邊長為200m的菱形池塘ABCD,塘邊AB與AD的夾角為60°,擬架設三條網隔BE,BF,EF,把池塘分成幾個不同區域,其中網隔BE與BF相互垂直,E,F兩點分別在塘邊AD和DC上,區域BEF為荷花種植區域.記∠ABE=![]() ,荷花種植區域的面積為Sm2.
,荷花種植區域的面積為Sm2.
(1)求S關于![]() 的函數關系式;
的函數關系式;
(2)求S的最小值.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某二手車直賣網站對其所經營的一款品牌汽車的使用年數x與銷售價格y(單位:萬元,輛)進行了記錄整理,得到如下數據:

(I)畫散點圖可以看出,z與x有很強的線性相關關系,請求出z與x的線性回歸方程(回歸系數![]() 精確到0.01);
精確到0.01);
(II)求y關于x的回歸方程,并預測某輛該款汽車當使用年數為10年時售價約為多少.
參考公式:
參考數據:
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業生產某種產品,為了提高生產效益,通過引進先進的生產技術和管理方式進行改革,并對改革后該產品的產量x(萬件)與原材料消耗量y(噸)及100件產品中合格品與不合格品數量作了記錄,以便和改革前作對照分析,以下是記錄的數據:
表一:改革后產品的產量和相應的原材料消耗量
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
表二:改革前后定期抽查產品的合格數與不合格數
合格品的數量 | 不合格品的數量 | 合計 | |
改革前 | 90 | 10 | 100 |
改革后 | 85 | 15 | 100 |
合計 | 175 | 25 | 200 |
(1)請根據表一提供數據,用最小二乘法求出y關于x的線性回歸方程![]() .
.
(2)已知改革前生產7萬件產品需要6.5噸原材料,根據回歸方程預測生產7萬件產品能夠節省多少原材料?
(3)請根據表二提供的數據,判斷是否有90%的把握認為“改革前后生產的產品的合格率有差異”?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xoy中,以坐標原點O為極點,x軸正半軸為極軸建立極坐標系。已知曲線C的極坐標方程為![]() ,過點
,過點![]() 的直線l的參數方程為
的直線l的參數方程為 (為參數),直線l與曲線C交于M、N兩點。
(為參數),直線l與曲線C交于M、N兩點。
(1)寫出直線l的普通方程和曲線C的直角坐標方程:
(2)若![]() 成等比數列,求a的值。
成等比數列,求a的值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)是定義在R上的奇函數,且當x≥0時,f(x)=x2,對任意的x∈[t,t+2]不等式f(x+t)≥2f(x)恒成立,那么實數t的取值范圍是( )
A. [![]() ,+∞) B. [2,+∞) C. (0,
,+∞) B. [2,+∞) C. (0,![]() ] D. [0,
] D. [0,![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一只紅螞蟻與一只黑螞蟻在一個單位圓(半徑為1的圓)上爬動,若兩只螞蟻均從點A(1,0)同時逆時針勻速爬動,若紅螞蟻每秒爬過α角,黑螞蟻每秒爬過β角(其中0°<α<β<180°),如果兩只螞蟻都在第14秒時回到A點,并且在第2秒時均位于第二象限,求α,β的值.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com