【題目】已知函數
.
（1）求
的單調區間；
（2）若的圖象與
軸有三個交點，求實數
的取值范圍.
【答案】（1）單調遞增區間是
；單調遞減區間是
；（2）
【解析】
（1）優先確定定義域，利用導數
，函數單調遞增，
，函數單調遞減，求得單調區間；
（2）利用轉化思想將要求轉化為函數
與函數
的圖象有三個不同交點，進而應位于函數
的兩個極值之間，再利用導數求得函數的極值即可求得答案.
（1）因為函數
，則定義域為R，
且
令
，所以函數
在區間上單調遞增；
令
或
，所以函數在區間上單調遞減；
故函數的單調遞增區間是；單調遞減區間是.
（2）條件中的圖象與
軸有三個交點，等價于
有三個不同的根，進而等價于函數與函數的圖象有三個不同交點，
因為
，且定義域為R，
令
，求得
或3
所以有
x |
| -1 |
| 3 |
|
| + | 0 | - | 0 | + |
|
| 極大值 |
| 極小值 |
|
所以函數在處取得極大值，為
；在
處取得極小值，為
，
因為函數與函數的圖象有三個不同交點，則應位于函數的兩個極值之間，則
故實數
的取值范圍為
千里馬走向假期期末仿真試卷寒假系列答案科目：高中數學 來源： 題型：
【題目】已知圓
，定點
，
為圓上任意一點,線段
的垂直平分線
和半徑
相交于點
，當點在圓上運動時，點的軌跡為曲線
.
（1）求曲線的方程;
（2）若過定點
的直線交曲線于不同的兩點
，
（點在點
，之間），且滿足
，求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知空間幾何體ABCDE中，△BCD與△CDE均是邊長為2的等邊三角形，△ABC是腰長為3的等腰三角形，平面CDE⊥平面BCD，平面ABC⊥平面BCD.
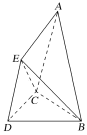
(1)試在平面BCD內作一條直線，使得直線上任意一點F與E的連線EF均與平面ABC平行，并給出證明；
(2)求三棱錐E－ABC的體積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列說法正確的是（）
A. “
，若
，則
且
”是真命題
B. 在同一坐標系中，函數
與
的圖象關于
軸對稱．
C. 命題“
，使得
”的否定是“
，都有
”
D. 
，“
”是“
”的充分不必要條件
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對數函數g（x）=1ogax（a＞0，a≠1）和指數函數f（x）=ax（a＞0，a≠1）互為反函數．已知函數f（x）=3x，其反函數為y=g（x）．
（Ⅰ）若函數g（kx2+2x+1）的定義域為R，求實數k的取值范圍；
（Ⅱ）若0＜x1＜x2且|g（x1）|=|g（x2）|，求4x1+x2的最小值；
（Ⅲ）定義在I上的函數F（x），如果滿足：對任意x∈I，總存在常數M＞0，都有-M≤F（x）≤M成立，則稱函數F（x）是I上的有界函數，其中M為函數F（x）的上界．若函數h（x）=
，當m≠0時，探求函數h（x）在x∈[0，1]上是否存在上界M，若存在，求出M的取值范圍，若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一個袋中有4個大小相同的小球，其中紅球1個，白球2個，黑球1個，現從袋中有放回地取球，每次隨機取一個，求
（1）連續取兩次都是白球的概率；
（2）若取一個紅球記2分，取一個白球記1分，取一個黑球記0分，連續取三次分數之和為4分的概率.（本小題基本事件總數較多不要求列舉，但是所求事件含的基本事件要列舉）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
