
【題目】若函數![]() 滿足:對于任意正數
滿足:對于任意正數![]() ,
,![]() ,都有
,都有![]() ,
,![]() ,且
,且![]() ,則稱函數
,則稱函數![]() 為“速增函數”.
為“速增函數”.
(1)試判斷函數![]() 與
與![]() 是否是“速增函數”;
是否是“速增函數”;
(2)若函數![]() 為“速增函數”,求
為“速增函數”,求![]() 的取值范圍;
的取值范圍;
(3)若函數![]() 為“速增函數”,且
為“速增函數”,且![]() ,求證:對任意
,求證:對任意![]() ,都有
,都有![]() .
.
【答案】(1)![]() 是,
是,![]() 不是;(2)
不是;(2)![]() ;(3)證明見解析
;(3)證明見解析
【解析】
(1)![]() 根據定義進行判斷即可,
根據定義進行判斷即可,![]() 利用特殊值,舉出反例;
利用特殊值,舉出反例;
(2)根據定義可知![]() ,即
,即![]() 對一切正數
對一切正數![]() 恒成立,可得
恒成立,可得![]() ,由
,由![]() ,可得
,可得
![]() 得出
得出![]() ,最后求出
,最后求出![]() 的范圍;
的范圍;
(3)根據定義,令![]() ,可知
,可知![]() ,即
,即![]() ,故對于正整數
,故對于正整數![]() 與正數
與正數![]() ,都有
,都有![]() ,進而得出結論.
,進而得出結論.
(1)對于函數![]() ,當
,當![]() ,
,![]() 時,
時,![]() ,
,
又![]() ,
,
所以![]() ,
,
故![]() 是“速增函數”.
是“速增函數”.
對于函數![]() ,當
,當![]() 時,
時,![]() ,
,
故![]() 不是“速增函數”.
不是“速增函數”.
(2)當![]() ,
,![]() 時,由
時,由![]() 是“速增函數”,
是“速增函數”,
可知![]() ,即
,即![]() 對一切正數
對一切正數![]() 恒成立,
恒成立,
又![]() ,可得
,可得![]() 對一切正數
對一切正數![]() 恒成立,所以
恒成立,所以![]() .
.
由![]() ,可得
,可得![]() ,
,
即![]()
![]() ,
,
故![]() ,又
,又![]() ,故
,故![]() ,
,
由![]() 對一切正數
對一切正數![]() ,
,![]() 恒成立,可得
恒成立,可得![]() ,即
,即![]() .
.
綜上可知,![]() 的取值范圍是
的取值范圍是![]() .
.
(3)由函數![]() 為“速增函數”,可知對于任意正數
為“速增函數”,可知對于任意正數![]() ,
,![]() ,
,
都有![]() ,
,![]() ,且
,且![]() ,
,
令![]() ,可知
,可知![]() ,即
,即![]() ,
,
故對于正整數![]() 與正數
與正數![]() ,都有
,都有![]() ,
,
對任意![]() ,
,![]() ,可得
,可得![]() ,又
,又![]() ,
,
所以![]() ,
,
同理![]() ,
,
故![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】定義在![]() 上的函數
上的函數![]() 若滿足:①對任意
若滿足:①對任意![]() 、
、![]() ,都有
,都有![]() ;②對任意
;②對任意![]() ,都有
,都有![]() ,則稱函數
,則稱函數![]() 為“中心捺函數”,其中點
為“中心捺函數”,其中點![]() 稱為函數
稱為函數![]() 的中心.已知函數
的中心.已知函數![]() 是以
是以![]() 為中心的“中心捺函數”,若滿足不等式
為中心的“中心捺函數”,若滿足不等式![]() ,當
,當![]() 時,
時,![]() 的取值范圍為( )
的取值范圍為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某射擊小組有甲、乙、丙三名射手,已知甲擊中目標的概率是![]() ,甲、丙二人都沒有擊中目標的概率是
,甲、丙二人都沒有擊中目標的概率是![]() ,乙、丙二人都擊中目標的概率是
,乙、丙二人都擊中目標的概率是![]() .甲乙丙是否擊中目標相互獨立.
.甲乙丙是否擊中目標相互獨立.
(1)求乙、丙二人各自擊中目標的概率;
(2)設乙、丙二人中擊中目標的人數為X,求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于定義在![]() 上的函數
上的函數![]() ,若存在正常數
,若存在正常數![]() 、
、![]() ,使得
,使得![]() 對一切
對一切![]() 均成立,則稱
均成立,則稱![]() 是“控制增長函數”.在以下四個函數中:①
是“控制增長函數”.在以下四個函數中:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .是“控制增長函數”的有( )個
.是“控制增長函數”的有( )個
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了豐富學生活動,在體育課上,體育教師設計了一個游戲,讓甲、乙、丙三人各抓住橡皮帶的一端,甲站在直角![]() 斜邊
斜邊![]() 的中點
的中點![]() 處,乙站在
處,乙站在![]() 處,丙站在
處,丙站在![]() 處.游戲開始,甲不動,乙、丙分別以
處.游戲開始,甲不動,乙、丙分別以![]() 和
和![]() 的速度同時出發,勻速跑向終點
的速度同時出發,勻速跑向終點![]() 和
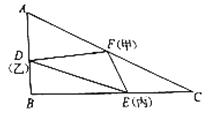
和![]() ,運動過程中繃緊的橡皮帶圍成一個如圖所示的
,運動過程中繃緊的橡皮帶圍成一個如圖所示的![]() .(規定:只要有一人跑到終點,游戲就結束,且
.(規定:只要有一人跑到終點,游戲就結束,且![]() ).已知
).已知![]() 長為
長為![]() ,
,![]() 長為
長為![]() ,記經過
,記經過![]() 后
后![]() 的面積為
的面積為![]() .
.
(1)求![]() 關于
關于![]() 的函數表示,并求出
的函數表示,并求出![]() 的取值范圍;
的取值范圍;
(2)當游戲進行到![]() 時,體育教師宣布停止,求此時
時,體育教師宣布停止,求此時![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com