Question

【題目】如圖，四邊形是平行四邊形，平面⊥平面，，，，，，，．

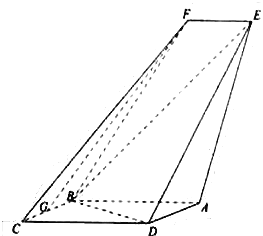
(Ⅰ)求證：平面；

(Ⅱ)求直線與平面所成角的正弦值.

Answer 1

【答案】（1）見解析；（2）直線與平面所成角的正弦值為.

【解析】

（1）利用中位線定理，先證明四邊形是平行四邊形，可得，再根據線面平行的判定定理即可證明；(2) 先判斷出直線與平面所成角即為直線與平面所成角, 過點作于點，連接，又可證明平面，所以直線與平面所成角即為，再根據余弦定理和解直角三角形即可求出結論.

（1）取的中點為，連接，在中，

因為是的中點，所以且，

又因為，所以且，

即四邊形是平行四邊形，所以，

又平面，平面，

所以平面.

（2）在中，，由余弦定理可，

進而可得，即，

又因為平面平面平面；平面平面，

所以平面.

又因為平面，

所以平面平面.

因為，

所以直線與平面所成角即為直線與平面所成角.

過點作于點，連接，

又因為平面平面，

所以平面，

所以直線與平面所成角即為.

在中，，由余弦定理可得，

所以，因此，

在中，，所以直線與平面所成角的正弦值為．