
【題目】已知函數![]()
(1)若直線![]() 與
與![]() 的圖象相切,求實數
的圖象相切,求實數![]() 的值;
的值;
(2)設![]() ,討論曲線
,討論曲線![]() 與曲線
與曲線![]() 公共點的個數;
公共點的個數;
(3)設![]() ,比較
,比較![]() 與
與![]() 的大小,并說明理由.
的大小,并說明理由.
【答案】(1)![]() (2)答案不唯一,詳情見解析(3)
(2)答案不唯一,詳情見解析(3)![]() ,證明見解析
,證明見解析
【解析】
(1)設切點為![]() ,由
,由![]() ,切點過直線
,切點過直線![]() 聯立求解即可;
聯立求解即可;
(2)求曲線![]() 與曲線
與曲線![]() 公共點的個數即求
公共點的個數即求![]() 與
與![]() 的公共點個數,通過研究導數性質確定函數
的公共點個數,通過研究導數性質確定函數![]() 增減性,討論
增減性,討論![]() 與函數最值點大小即可;
與函數最值點大小即可;
(3)可先通過試值,預判![]()
![]() ,原不等式可表示為
,原不等式可表示為![]() ,變形得
,變形得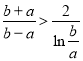 ,再令
,再令![]() ,再結合換元法和構造函數法即可求證
,再結合換元法和構造函數法即可求證
(1)設切點為![]() ,則
,則![]() ,又切點過直線
,又切點過直線![]() ,所以
,所以![]() ,聯立求解可得
,聯立求解可得![]() ,
,![]() ;
;
(2)原題可等價轉化為求![]() 與
與![]() 的公共點個數,
的公共點個數,
令![]() ,令
,令![]() 可得
可得![]() ,當
,當![]() 時,
時,![]() ,
,![]() 單增;當
單增;當![]() 時,
時,![]() ,
,![]() 單減;故
單減;故![]() ,
,
又當![]() 時,
時,![]() ,當
,當![]() 時,由冪函數的增長性遠遠大于對數函數可知,
時,由冪函數的增長性遠遠大于對數函數可知,![]() ,故
,故![]() 的大致圖像為
的大致圖像為
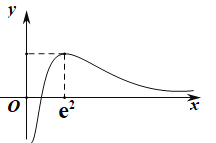
當![]() 時,
時,![]() 與
與![]() 有兩個共同點;
有兩個共同點;
當![]() 時,
時,![]() 與
與![]() 有一個公共點;
有一個公共點;
當![]() 時,
時,![]() 與
與![]() 無公共點;
無公共點;
(3)![]() ,證明如下,要證
,證明如下,要證![]() ,即證
,即證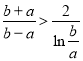 ,即
,即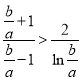 ,令
,令![]() ,則原式變為
,則原式變為![]() ,即
,即![]() ,
,
令![]() ,則
,則 ,故
,故![]() 在
在![]() 上單增,所以當
上單增,所以當![]() ,又
,又![]() ,所以
,所以![]() 恒成立,原式得證
恒成立,原式得證


科目:高中數學 來源: 題型:
【題目】為了比較注射![]() ,
,![]() 兩種藥物后產生的皮膚皰疹的面積,選200只家兔做試驗,將這200只家兔隨機地分成兩組,每組100只,其中一組注射藥物
兩種藥物后產生的皮膚皰疹的面積,選200只家兔做試驗,將這200只家兔隨機地分成兩組,每組100只,其中一組注射藥物![]() ,另一組注射藥物
,另一組注射藥物![]() .下表1和表2分別是注射藥物
.下表1和表2分別是注射藥物![]() 和藥物
和藥物![]() 的試驗結果.(皰疹面積單位:
的試驗結果.(皰疹面積單位:![]() )
)
表1:注射藥物![]() 后皮膚皰疹面積的頻數分布表
后皮膚皰疹面積的頻數分布表
皰疹面積 |
|
|
|
|
頻數 | 30 | 40 | 20 | 10 |
表2:注射藥物![]() 后皮膚皰疹面積的頻數分布表
后皮膚皰疹面積的頻數分布表
皰疹面積 |
|
|
|
|
|
頻數 | 10 | 25 | 20 | 30 | 15 |
附: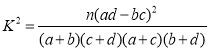
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
(1)完成下面頻率分布直方圖,并比較注射兩種藥物后皰疹面積的中位數大小(不必算出中位數);
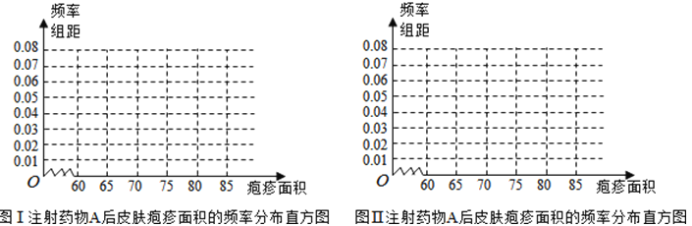
(2)完成下面![]() 列聯表,并回答能否有99.9%的把握認為“注射藥物
列聯表,并回答能否有99.9%的把握認為“注射藥物![]() 后的皰疹面積與注射藥物
后的皰疹面積與注射藥物![]() 后的皰疹面積有差異”.
后的皰疹面積有差異”.
表3:
皰疹面積小于 | 皰疹面積不小于 | 合計 | |
注射藥物 |
|
| |
注射藥物 |
|
| |
合計 |
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】七巧板是一種古老的中國傳統智力玩具,顧名思義,是由七塊板組成的.而這七塊板可拼成許多圖形.如圖中的正方形七巧板就是由五塊等腰直角三角形、一塊正方形和一塊平行四邊形組成的.若向正方形內隨機的拋10000顆小米粒(大小忽略不計),則落在陰影部分的小米粒大約為( )
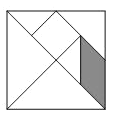
A.3750B.2500C.1875D.1250
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 為等邊三角形,邊長為2,
為等邊三角形,邊長為2,![]() 為等腰直角三角形,
為等腰直角三角形,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面ABCD.
平面ABCD.
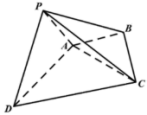
(1)證明:![]() 平面PAD;
平面PAD;
(2)求平面PAD與平面PBC所成銳二面角的余弦值;
(3)棱PD上是否存在一點E,使得![]() 平面PBC?若存在,求出
平面PBC?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知半徑為5的圓的圓心在x軸上,圓心的橫坐標是整數,且與直線4x+3y﹣29=0相切.
(1)求圓的方程;
(2)設直線ax﹣y+5=0(a>0)與圓相交于A,B兩點,求實數a的取值范圍;
(3)在(2)的條件下,是否存在實數a,使得弦AB的垂直平分線l過點P(﹣2,4),若存在,求出實數a的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,圓
中,圓![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以
為參數),以![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建極坐標系,直線
軸的非負半軸為極軸建極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]()
(Ⅰ)求![]() 的極坐標方程;
的極坐標方程;
(Ⅱ)射線![]() 與圓C的交點為
與圓C的交點為![]() 與直線
與直線![]() 的交點為
的交點為![]() ,求
,求![]() 的范圍.
的范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com