
【題目】某企業有甲、乙兩條生產線生產同種產品,現隨機從這兩條生產線上各抽取20件產品檢測質量(單位:克),質量值落在![]() ,
, ![]() 的產品為三等品,質量值落在
的產品為三等品,質量值落在![]() ,
, ![]() 的產品為二等品,質量值落在
的產品為二等品,質量值落在![]() 的產品為一等品.下表為從兩條生產線上各抽取的20件產品的質量檢測情況,將頻率視為概率,從甲生產線上隨機抽取1件產品,為二等品的概率為0.2.
的產品為一等品.下表為從兩條生產線上各抽取的20件產品的質量檢測情況,將頻率視為概率,從甲生產線上隨機抽取1件產品,為二等品的概率為0.2.
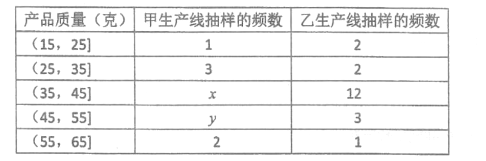
(1)求![]() 的值;
的值;
(2)現從兩條生產線上的三等品中各抽取1件,求這兩件產品的質量均在![]() 的概率;
的概率;
(3)估算甲生產線20個數據的中位數(保留3位有效數字).
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)39.6
;(3)39.6
【解析】試題分析:(1)根據從甲生產線上隨機抽取1件產品,為二等品的概率為0.2,得到式子為![]() ,進而得到值;(2)根據古典概型的計算公式得到,先得到從兩條生產線上的三等品中各抽取1件,所有可能情況是共9種情況,這兩件產品的質量均在
,進而得到值;(2)根據古典概型的計算公式得到,先得到從兩條生產線上的三等品中各抽取1件,所有可能情況是共9種情況,這兩件產品的質量均在![]() 上的可能情況是:
上的可能情況是: ![]() ,共2種情況,進而得到概率值;(3)根據中位數的概念得到
,共2種情況,進而得到概率值;(3)根據中位數的概念得到![]() ,進而求出參數值、
,進而求出參數值、
解析:
(1)由題意![]() 所以
所以![]() ,
, ![]() ,
,
(2)甲生產線產品質量在![]() 上的數據記為
上的數據記為![]() ,在
,在![]() 上的數據記為
上的數據記為![]() ,
, ![]()
乙生產線產品質量在![]() 上的數據記為
上的數據記為![]() ,在
,在![]() 上的數據記為
上的數據記為![]()
從兩條生產線上的三等品中各抽取1件,所有可能情況是: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,共9種情況
,共9種情況
這兩件產品的質量均在![]() 上的可能情況是:
上的可能情況是: ![]() ,共2種情況
,共2種情況
所以,從兩條生產線上的三等品中各抽取1件,求這兩件產品的質量均在![]() 的概率
的概率![]()
(3)設甲生產線20個數據的中位數是![]()
則由題意![]()
解得![]() (克)
(克)
所以甲生產線20個數據的中位數約是39.6克.


 導學與測試系列答案
導學與測試系列答案 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)
如圖,在四棱錐P—ABCD中,側面PAD⊥底面ABCD,側棱PA=PD=![]() ,底面ABCD為直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O為AD中點.
,底面ABCD為直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O為AD中點.
(Ⅰ)求證:PO⊥平面ABCD;
(Ⅱ)求異面直線PB與CD所成角的余弦值;
(Ⅲ)求點A到平面PCD的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左右焦點分別為
的左右焦點分別為![]() ,
,![]() ,左頂點為
,左頂點為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,且
上,且![]() 的面積為
的面積為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過原點![]() 且與
且與![]() 軸不重合的直線交橢圓
軸不重合的直線交橢圓![]() 于
于![]() ,
,![]() 兩點,直線
兩點,直線![]() 分別與
分別與![]() 軸交于點
軸交于點![]() ,
,![]() ,.求證:以
,.求證:以![]() 為直徑的圓恒過交點
為直徑的圓恒過交點![]() ,
,![]() ,并求出
,并求出![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有![]() 六支足球隊參加單循環比賽(即任意兩支球隊只踢一場比賽),第一周的比賽中
六支足球隊參加單循環比賽(即任意兩支球隊只踢一場比賽),第一周的比賽中![]() ,各踢了
,各踢了![]() 場,
場, ![]() 各踢了
各踢了![]() 場,
場, ![]() 踢了
踢了![]() 場,且
場,且![]() 隊與
隊與![]() 隊未踢過,
隊未踢過, ![]() 隊與
隊與![]() 隊也未踢過,則在第一周的比賽中,
隊也未踢過,則在第一周的比賽中, ![]() 隊踢的比賽的場數是( )
隊踢的比賽的場數是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在扶貧活動中,為了盡快脫貧(無債務)致富,企業甲將經營情況良好的某種消費品專賣店以![]() 萬元的優惠價轉讓給了尚有
萬元的優惠價轉讓給了尚有![]() 萬元無息貸款沒有償還的小型企業乙,并約定從該店經營的利潤中,首先保證企業乙的全體職工每月最低生活費的開支
萬元無息貸款沒有償還的小型企業乙,并約定從該店經營的利潤中,首先保證企業乙的全體職工每月最低生活費的開支![]() 元后,逐步償還轉讓費(不計息).在甲提供的資料中有:①這種消費品的進價為每件
元后,逐步償還轉讓費(不計息).在甲提供的資料中有:①這種消費品的進價為每件![]() 元;②該店月銷量
元;②該店月銷量![]() (百件)與銷售價格
(百件)與銷售價格![]() (元)的關系如圖所示;③每月需各種開支
(元)的關系如圖所示;③每月需各種開支![]() 元.
元.
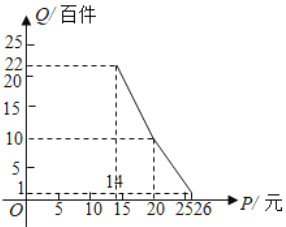
(1)當商品的價格為每件多少元時,月利潤扣除職工最低生活費的余額最大?并求最大余額;
(2)企業乙只依靠該店,最早可望在幾年后脫貧?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com