
【題目】△ABC中,角A,B,C的對邊分別為a,b,c,且cosC= ![]() .
.
(1)求角B的大小;
(2)若BD為AC邊上的中線,cosA= ![]() ,BD=
,BD= ![]() ,求△ABC的面積.
,求△ABC的面積.
【答案】
(1)解:2bcosC+c=2a,由正弦定理,得2sinBcosC+sinC=2sinA.
∵A+B+C=π,∴sinA=sin(B+C)=sinBcosC+cosBsinC,
∴2sinBcosC+sinC=2(sinBcosC+cosBsinC),∴sinC=2cosBsinC,
∵0<C<π,∴sinC≠0,∴ ![]() .
.
又∵0<B<π,∴B= ![]()
(2)解:在△ABD中,由余弦定理得 ![]() =c2+
=c2+ ![]() ﹣2c×
﹣2c× ![]() cosA,
cosA,
∴ ![]() =c2+
=c2+ ![]() ﹣
﹣ ![]() bc,①,
bc,①,
在△ABC中,由正弦定理得 ![]() =
= ![]() ,由已知得sinA=
,由已知得sinA= ![]() .
.
∴sinC=sin(A+B)=sinAcosB+cosAsinB= ![]() ,
,
∴c= ![]() b…②,
b…②,
由①,②解得b=7,c=5,
∴S△ABC= ![]() bcsinA=10
bcsinA=10 ![]()
【解析】(1)利用正弦定理、和差公式即可得出.(2)在△ABD中,由余弦定理得 ![]() =c2+
=c2+ ![]() ﹣2c×
﹣2c× ![]() cosA,在△ABC中,由正弦定理得
cosA,在△ABC中,由正弦定理得 ![]() =
= ![]() ,由已知得sinA=
,由已知得sinA= ![]() .再利用sinC=sin(A+B)=sinAcosB+cosAsinB=
.再利用sinC=sin(A+B)=sinAcosB+cosAsinB= ![]() ,聯立解出.
,聯立解出.
【考點精析】掌握正弦定理的定義和余弦定理的定義是解答本題的根本,需要知道正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】過點(0,4),斜率為﹣1的直線與拋物線y2=2px(p>0)交于兩點A、B,且弦|AB|的長度為4![]() .
.
(1)求p的值;
(2)求證:OA⊥OB(O為原點).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】霧霾天氣對城市環境造成很大影響,按照國家環保部發布的標準:居民區的PM2.5(大氣中直徑小于或等于2.5微米的顆粒物)年平均濃度不得超過35微克/立方米.某市環保部門加強了對空氣質量的監測,抽取某居民區監測點的20天PM2.5的24小時平均濃度的監測數據,制成莖葉圖,如圖:
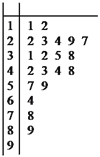
(Ⅰ)完成如下頻率分布表,并在所給的坐標系中畫出![]() 的頻率分布直方圖;
的頻率分布直方圖;
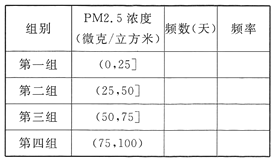
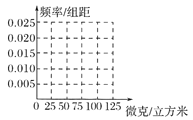
(Ⅱ)從樣本中PM2.5的24小時平均濃度超過50微克/立方米的天數中,隨機抽取2天,求恰好有一天PM2.5的24小時平均濃度超過75微克/立方米的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在區間[﹣1,1]上任取兩個數a,b,在下列條件時,分別求不等式x2+2ax+b2≥0恒成立時的概率:
(1)當a,b均為整數時;
(2)當a,b均為實數時.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位招聘職工分為筆試和面試兩個環節,將筆試成績合格(滿分100分,及格60分,精確到個位數)的應聘者進行統計,得到如下的頻率分布表:
分組 | 頻數 | 頻率 |
[60,70] |
| 0.16 |
(70,80] | 22 |
|
(80,90] | 14 | 0.28 |
(90,100] |
|
|
合計 | 50 | 1 |
(Ⅰ)確定表中![]() 的值(直接寫出結果,不必寫過程)
的值(直接寫出結果,不必寫過程)
(Ⅱ)面試規定,筆試成績在80分(不含80分)以上者可以進入面試環節,面試時又要分兩關,首先面試官依次提出4個問題供選手回答,并規定,答對2道題就終止回答,通過第一關可以進入下一關,如果前三題均沒有答對,則不再回答第四題并且不能進入下一關,假定某選手獲得面試資格的概率與答對每道題的概率相等.
![]() 求該選手答完3道題而通過第一關的概率;
求該選手答完3道題而通過第一關的概率;
![]() 記該選手在面試第一關中的答題個數為X,求X的分布列及數學期望.
記該選手在面試第一關中的答題個數為X,求X的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學在研究函數f(x)= ![]() (x∈R)時,分別給出下面幾個結論:
(x∈R)時,分別給出下面幾個結論:
①f(﹣x)+f(x)=0在x∈R時恒成立;
②函數f(x)的值域為(﹣1,1);
③若x1≠x2 , 則一定有f(x1)≠f(x2);
④函數g(x)=f(x)﹣x在R上有三個零點.
其中正確結論的序號有 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C的方程為: ![]() =1(a>0),其焦點在x軸上,離心率e=
=1(a>0),其焦點在x軸上,離心率e= ![]() .
.
(1)求該橢圓的標準方程;
(2)設動點P(x0 , y0)滿足 ![]() ,其中O為坐標原點,M,N是橢圓C上的點,直線OM與ON的斜率之積為﹣
,其中O為坐標原點,M,N是橢圓C上的點,直線OM與ON的斜率之積為﹣ ![]() ,求證:x02+2y02為定值.
,求證:x02+2y02為定值.
(3)在(2)的條件下,問:是否存在兩個定點A,B,使得|PA|+|PB|為定值?若存在,給出證明;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是我國2008年至2014年生活垃圾無害化處理量(單位:億噸)的折線圖 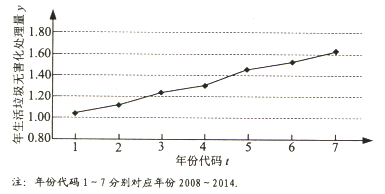
(Ⅰ)由折線圖看出,可用線性回歸模型擬合y與t的關系,請用相關系數加以說明;
(Ⅱ)建立y關于t的回歸方程(系數精確到0.01),預測2017年我國生活垃圾無害化處理量.
參考數據: ![]() =9.32,
=9.32, ![]() yi=40.17,
yi=40.17, ![]() =0.55,
=0.55, ![]() ≈2.646.
≈2.646.
參考公式:相關系數r= 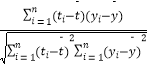 回歸方程
回歸方程 ![]() =
= ![]() +
+ ![]() t 中斜率和截距的最小二乘估計公式分別為:
t 中斜率和截距的最小二乘估計公式分別為: ![]() =
= 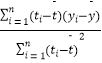 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
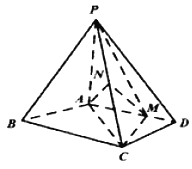
【題目】如圖,在四棱錐![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,且,
,且, ![]() ,
, ![]() ,
, ![]() 為線段
為線段![]() 上一點,
上一點, ![]() ,且
,且![]() 為
為![]() 的中點.
的中點.
(Ⅰ)證明: ![]() 平面
平面![]() ;
;
(Ⅱ)求證:平面![]() 平面
平面![]() ;
;
(Ⅲ)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com