
【題目】已知函數![]() 是奇函數.
是奇函數.
(1)求a的值和函數f(x)的定義域;
(2)解不等式f(-m2+2m-1)+f(m2+3)<0.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】分析:(1)根據函數奇偶性的定義建立方程即可求出a,根據分式函數的意義即可求出函數的定義域.
(2)根據函數奇偶性和單調性的性質將不等式進行轉化求解即可.
詳解:
(1)因為函數f(x)=![]() +a是奇函數,所以f(-x)=-f(x),
+a是奇函數,所以f(-x)=-f(x),
即![]() +a=
+a=![]() -a,即
-a,即![]() =
=![]() ,從而有1-a=a,解得a=
,從而有1-a=a,解得a=![]() .
.
又2x-1≠0,所以x≠0,故函數f(x)的定義域為(-∞,0)∪(0,+∞).
(2)由f(-m2+2m-1)+f(m2+3)<0,得f(-m2+2m-1)<-f(m2+3),因為函數f(x)為奇函數,所以f(-m2+2m-1)<f(-m2-3).
由(1)可知函數f(x)在(0,+∞)上是減函數,從而在(-∞,0)上是減函數,又-m2+2m-1<0,-m2-3<0,所以-m2+2m-1>-m2-3,且![]() 解得m>-1,且
解得m>-1,且![]() ,所以不等式的解集為
,所以不等式的解集為![]()


科目:高中數學 來源: 題型:
【題目】已知動點M(x,y)滿足![]() ,點M的軌跡為曲線E.
,點M的軌跡為曲線E.
(1)求E的標準方程;
(2)過點F(1,0)作直線交曲線E于P,Q兩點,交![]() 軸于R點,若
軸于R點,若![]() ,證明:
,證明:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x|x-4| (x∈R)
(1)用分段形式寫出函數f(x)的表達式,并作出函數f(x)的圖象;
(2) 根據圖象指出f(x)的單調區間,并寫出不等式f(x)>0的解集;
(3) 若h(x)=f(x)-k有三個零點,寫出k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】知雙曲線 ![]() ﹣
﹣ ![]() =1(a>0,b>0),A1、A2是實軸頂點,F是右焦點,B(0,b)是虛軸端點,若在線段BF上(不含端點)存在不同的兩點Pi=(1,2),使得△PiA1A2(i=1,2)構成以A1A2為斜邊的直角三角形,則雙曲線離心率e的取值范圍是( )
=1(a>0,b>0),A1、A2是實軸頂點,F是右焦點,B(0,b)是虛軸端點,若在線段BF上(不含端點)存在不同的兩點Pi=(1,2),使得△PiA1A2(i=1,2)構成以A1A2為斜邊的直角三角形,則雙曲線離心率e的取值范圍是( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() )
)
C.(1, ![]() )
)
D.( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知矩形ABCD與直角梯形ABEF,∠DAF=∠FAB=90°,點G為DF的中點,AF=EF= ![]() ,P在線段CD上運動.
,P在線段CD上運動. 
(1)證明:BF∥平面GAC;
(2)當P運動到CD的中點位置時,PG與PB長度之和最小,求二面角P﹣CE﹣B的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的幾何體ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥ AB,M是EC上的點(不與端點重合),F為DA上的點,N為BE的中點.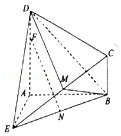
(Ⅰ)若M是EC的中點,AF=3FD,求證:FN∥平面MBD;
(Ⅱ)若平面MBD與平面ABD所成角(銳角)的余弦值為 ![]() ,試確定點M在EC上的位置.
,試確定點M在EC上的位置.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=Acos(ωx+φ)(A>0,ω>0,﹣π<φ<0)的部分圖象如圖所示,為了得到g(x)=Acosωx的圖象,只需將函數y=f(x)的圖象( ) 
A.向左平移 ![]() 個單位長度
個單位長度
B.向左平移 ![]() 個單位長度
個單位長度
C.向右平移 ![]() 個單位長度
個單位長度
D.向右平移 ![]() 個單位長度
個單位長度
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com